Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng BĐT Cosi:
\(\sqrt{\left(p-a\right)\left(p-b\right)}\le\dfrac{p-a+p-b}{2}=\dfrac{c}{2}\)
\(\sqrt{\left(p-b\right)\left(p-c\right)}\le\dfrac{p-b+p-c}{2}=\dfrac{a}{2}\)
\(\sqrt{\left(p-c\right)\left(p-a\right)}\le\dfrac{p-c+p-a}{2}=\dfrac{b}{2}\)
\(\Rightarrow\left(p-a\right)\left(p-b\right)\left(p-c\right)\le\dfrac{1}{8}abc\)

Nhận xét: Tam giác ABC có a2 + b2 = c2 nên vuông tại C.
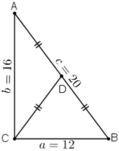
+ Diện tích tam giác: S = 1/2.a.b = 1/2.12.16 = 96 (đvdt)
+ Chiều cao ha: ha = AC = b = 16.
+ Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.
Bán kính đường tròn ngoại tiếp R = AB /2 = c/2 = 10.
+ Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = S/p.
Mà S = 96, p = (a + b + c) / 2 = 24 ⇒ r = 4.
+ Đường trung tuyến ma:
ma2 = (2.(b2 + c2) – a2) / 4 = 292 ⇒ ma = √292.

Cách làm sơ khảo:
Gọi các giao điểm của 3 đường đã cho. P là giao điểm của phân giác và trung tuyến
Q là giao điểm của trung tuyến và đường cao. R là giao điểm của phân giác và đường cao. Các điểm này đều biết tọa độ rồi.
Xét tam giác ABQ có QR vuông góc AB, AR vuông góc BQ suy ra R là trực tâm Nên có BR vuông góc AQ.
Gọi tọa độ điểm A(a,3-a). B(b, b+1)
Ta có 2 pt để tính a,b là tích vô hướng của BR.AQ=0 và véc tơ AB song song với véc tơ pháp cảu RQ chính là đường cao qua C
Tìm ra a,b.
Tìm ra điểm A,B
Gọi M là trung điểm của AC
Xét tan giác ABM có phân giác AP vuông góc với BM Suy ra P là trung điểm của BM
Tìm được tọa độ M. Từ đó tính ra tọa độ C