Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: △△ABC cân tại A ⇒⇒ ABCˆ=ACBˆABC^=ACB^ (1)
DF//AC ⇒⇒ DF//EC ⇒⇒ {ACBˆ=DFBˆ(2)FDIˆ=IECˆ(3){ACB^=DFB^(2)FDI^=IEC^(3)
Từ (1);(2) ⇒⇒ ABCˆ=DFBˆABC^=DFB^
⇒⇒ △△DFB cân tại D
⇒⇒ BD=DF.
Mà BD=CE(gt) ⇒⇒ CE=DF.
Xét △△FDI và △△CEI có:
DF=CE(cmt)
FDIˆ=IECˆFDI^=IEC^ (cmt)
DI=IE(I là trung điểm DE)
⇒⇒ △△FDI = △△CEI (c-g-c)
⇒⇒ FIDˆ=EICˆFID^=EIC^
Ta có: DICˆ+CIEˆDIC^+CIE^ = 180o
Mà FIDˆ=EICˆFID^=EIC^ (cmt)
⇒⇒ DICˆ+DIFˆDIC^+DIF^ = 180o
⇒⇒ FICˆ=1800FIC^=1800
Hay BICˆ=1800BIC^=1800
⇒⇒ 3 điểm B,I,C thẳng hàng (đpcm)

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

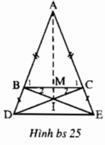
Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.