Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Vì BD là pg nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{AC}{AB+BC}=\dfrac{15}{25}=\dfrac{3}{5}\Rightarrow DC=6cm;AD=9cm\)
b, Ta có BD là pg, mà BD vuông BE
nên BE là pg ngoài tam giác ABC
\(\dfrac{EC}{AC}=\dfrac{AB}{BC}\Rightarrow EC=\dfrac{AB.AC}{BC}=\dfrac{45}{2}cm\)
a: Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/15=CD/10
=>AD/3=CD/2=(AD+CD)/(3+2)=15/5=3
=>AD=9cm; CD=6cm
b: BE vuông góc BD
=>BE là phân giác góc ngoài tại B
=>EC/EA=BC/BA
=>EC/(EC+15)=10/15=2/3
=>3EC=2EC+30
=>EC=30cm
a: Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/15=CD/10
=>AD/3=CD/2=(AD+CD)/(3+2)=15/5=3
=>AD=9cm; CD=6cm
b: BE vuông góc BD
=>BE là phân giác góc ngoài tại B
=>EC/EA=BC/BA
=>EC/(EC+15)=10/15=2/3
=>3EC=2EC+30
=>EC=30cm
Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B
Suy ra :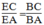 
( t/chất đường phân giác)
Suy ra: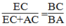 
⇒ EC.BA= BC (EC + AC)
Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC
Vậy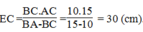 
a) ta có BD là pg => DA/DC=AB/AC=15/10=3/2
=> DA/3=DC/2=DA+DC/3+2=AC/5=15/5=3
=> DA=3.3=9 cm
DC=3.2=6 cm
b) ta có BE là pg ngoài=> EA/EC=AB/BC=15/10=3/2
=> EA/3=EC/2=EA-EC/3-2=AC/1=15/1=15
=> EC=15.2=30cm
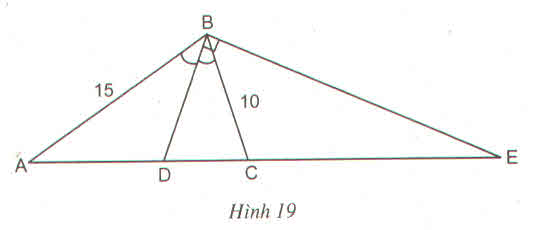
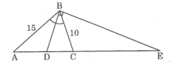
a) Theo đề bài ta có:
\(\dfrac{AD}{DC}=\dfrac{BA}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
\(\dfrac{AD}{AD+DC}=\dfrac{15}{15+10}hay\dfrac{AD}{AC}=\dfrac{15}{25}\)
=> AD = \(\dfrac{15.AC}{25}=\dfrac{15.15}{25}=9\left(cm\right)\)
DC = AC - AD = 15 - 9 = 6 (cm)
Vậy AD = 9cm; DC = 6cm.
b) Vì BD \(\perp\) BE nên BE là đường phân giác của góc ngoài tại đỉnh B.
Áp dụng tính chất đường phân giác của góc ngoài ta có:
\(\dfrac{EC}{EA}=\dfrac{EC}{EC+AC}=\dfrac{BC}{BA}\)
hay \(\dfrac{EC}{EC+15}=\dfrac{10}{15}=\dfrac{2}{3}\)
=> EC = 30 (cm)
Vậy EC = 30cm.