Đáp án A

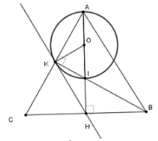
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

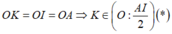
Xét tam giác OKA cân tại O (vì OA=OK=R) có:

O K A ^ = O A K ^  (1)

Xét tam giác CKB vuông tại K (vì  K B ⊥ A C ) có:

H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)

⇒ KH là trung tuyến ứng với cạnh huyền BC

⇒ H K C ^ = H C K ^   ( 2 )

Từ (1) và (2) suy ra  O K A ^ + H K C ^ = O A K ^ + H C K ^ = 90 o (vì  A H ⊥ B C )

Mà  O K A ^ + H K C ^ + O K H ^ = 180 o ⇒ O K H ^ = 90 o ⇒ O K ⊥ K H (**)

Từ (*) và (**) suy ra HK là tiếp tuyến của (O)

a, Chứng minh được  B K A ^ = 90 0

b, Gọi O là trung điểm AI

Ta có:

+ OK = OA =>  O K A ^ = O A K ^

+  O A K ^ = H B K ^ (cùng phụ  A C B ^ )

+ HB = HK =>  H B K ^ = H K B ^

=> O K A ^ = H K B ^ ⇒ H K O ^ = 90 0

a: Vì góc AKI=90 độ

nên K nằm trên đường tròn đường kính AI

b: Gọi G là trung điểm của AK

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

a: Vì góc AKI=90 độ

nên K nằm trên đường tròn đường kính AI

b: Gọi G là trung điểm của AK

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

a: Ta có: ΔBKC vuông tại K

mà KH là trung tuyến

nên KH=BH

=>ΔHBK cân tại H

b: góc BAH=90 độ-góc ABC

góc IAK=90 độ-góc ACB

mà góc ABC=góc ACB

nên góc BAH=góc IAK

c: Gọi G là trung điểm của AI

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

\(\left\{{}\begin{matrix}\widehat{DCA}=\widehat{HCA}\\\widehat{DCA}+\widehat{DAC}=90^0\\\widehat{HCA}+\widehat{HBA}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{HBA}=\widehat{DAC}\)

\(\left\{{}\begin{matrix}\widehat{DAC}+\widehat{BAE}=90^0\\\widehat{HBA}+\widehat{HAB}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{BAE}=\widehat{HAB}\)

Có \(\left\{{}\begin{matrix}AH=AE=R\\\widehat{BAE}=\widehat{HAB}\\\text{AB chung}\end{matrix}\right.\)  \(\Rightarrow\Delta AHB=\Delta AEB\)

\(\Rightarrow\widehat{E}=\widehat{H}=90^0\Rightarrow BE\) là tiếp tuyến

Cách chứng minh ^BAE=^HAB khó nghĩ thật ạ.

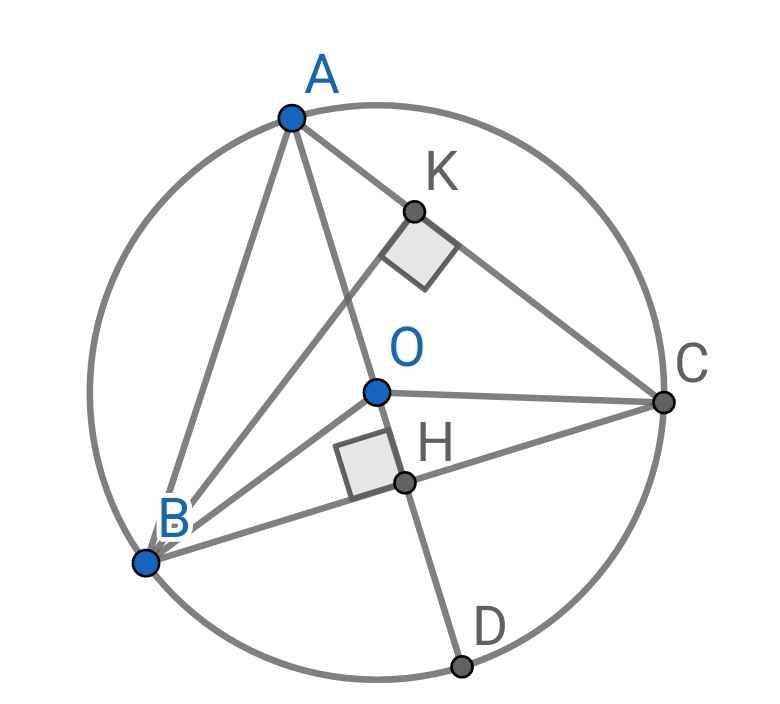 a) Ta có:

OB = OC (bán kính)

⇒ O nằm trên đường trung trực của BC (1)

Do ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung trực của ∆ABC

⇒ AH là đường trung trực của BC (2)

Từ (1) và (2) suy ra O ∈ AH

⇒ O ∈ AD

Vậy AD là đường kính của (O)

b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC

Do AH là đường trung trực của BC (cmt)

⇒ H là trung điểm của BC

⇒ CH = BC : 2

= 12 : 2

= 6 (cm)

∆AHC vuông tại H

⇒ AC² = AH² + CH² (Pytago)

⇒ AH² = AC² - CH²

= 10² - 6²

= 64

⇒ AH = 8 (cm)

⇒ sinACH = AH/AC

= 4/5

⇒ ACH ≈ 53⁰

⇒ BCK ≈ 53⁰

∆BCK vuông tại K

⇒ sinBCK = BK/BC

⇒ BK = BC.sinBCK

= 10.sin53⁰

≈ 8 (cm)