độ dài cạnh IH là :20:2=10(cm)

áp dụng định lí py-ta-go ta co:

\(EH^2=EI^2+IH^2=10^2+24^2=100+576=676\)

\(EH=\sqrt{676}\left(cm\right)\)

đề sai ko

mình ko bt

tam giác ABC có : BE; CF là trung tuyến và cắt nhau tại I

=> AI là trung tuyến (tc)

mà tam giác ABC cân tại A (Gt)

=> AI là phân giác của góc BAC (đl)

a)Xét\(\Delta ABC\)có:\(BE\)là đg trung tuyến xuất phát từ đỉnh\(B\left(GT\right)\)

\(CF\)là đg trung tuyến xuất phát từ đỉnh\(C\left(GT\right)\)

mà\(BE\)cắt\(CF\)tại\(I\)

\(\Rightarrow AI\)là đg trung tuyến xuất phát từ đỉnh\(A\)(Định lí về tính chất 3 đg trung tuyến của 1\(\Delta\))

mà\(\Delta ABC\)cân tại\(A\left(GT\right)\)

\(\Rightarrow AI\)vừa là đg trung tuyến vừa là đg p/g của\(\Delta ABC\)(Tính chất của tg cân)

b)Xét\(\Delta ABI\)và\(\Delta ACI\)có:

\(AI\)là cạnh chung

\(\widehat{BAI}=\widehat{CAI}\)(\(AI\)là tia p/g của\(\widehat{BAC}\))

\(AB=AC\)(\(\Delta ABC\)cân tại\(A\))

Do đó:\(\Delta ABI=\Delta ACI\left(c-g-c\right)\)

\(\Rightarrow\widehat{ABI}=\widehat{ACI}\)(2 cạnh t/ứ)

\(BI=CI\)(2 cạnh t/ứ)

Xét\(\Delta ABE\)và\(\Delta ACF\)có:

\(\widehat{ABE}=\widehat{ACF}\left(cmt\right)\)

​\(AB=AC\)​(\(\Delta ABC\)cân tại\(A\))

I là trung điểm của EF nên IE = IF = EF/2 = 5cm.

Ta có : 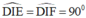 ⇒ ΔDIE vuông tại I

Theo định lý Pitago trong tam giác vuông DIE ta có :

DE2 = DI2 + EI2 ⇒ DI2 = DE2 – EI2 = 132 – 52 = 144 ⇒ DI = 12 (cm).

Vẽ điểm K sao cho D là trung điểm của GK ta tính được BK=CG=10; BG=6; GD=4; GK=8

BGK có 3 cạnh bằng 6;8;10 nên

(định lý Pytago đảo)