Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC

a ) Xét tam giác AMB và tam giác NMC có :
AM = MN ( gt )
Góc AMB = góc NMC ( đối đỉnh )
BM = MC ( vì AM là đường trung tuyến của BC )
=> Tam giác AMB = Tam giác NMC ( c.g.c )
=> Góc ABM = góc NCM ( 2 góc tương ứng )
Mà góc ABM = góc NCM so le trong
=> CN // AB
b ) Xét tam giác ABC và tam giác NCB có :
AB = NC ( tam giác AMB = tam giác NMC mà cạnh AB và NC là 2 cạnh tương ứng )
Góc ABC = góc NCB ( vì tam giác AMB = tam giác NMC mà góc ABC và góc NCB là 2 góc tương ứng )
AB là cạnh chung
=> Tam giác ABC = Tam giác NCB ( c.g.c )

a) Xét tam giác AMB và tam giác NMC có:
AM=MN (gt)
Góc AMB=góc NMC (đối đỉnh)
BM=MC(vì AM là đường trung tuyến của BC)
=> Tam giác AMB = tam giác NMC (c.g.c) => góc ABM=góc NCM ( 2 góc tương ứng )
mà góc ABM và góc NCM so le trong => CN//AB
b) Xét tam giác ABC và tam giác NCB có:
AB=NC (\(\Delta AMB=\Delta NMC\) mà cạnh AB và NC là 2 cạnh tương ứng)
Góc ABC = góc NCB ( \(\Delta AMB=\Delta NMC\) mà góc ABC và góc NCB là 2 góc tương ứng)
AB là cạnh chung
=> Tam giác ABC và tam giác NCB (c.g.c)
c) bạn tham khảo câu trả lời của mình ở đây: https://olm.vn/hoi-dap/question/827711.html
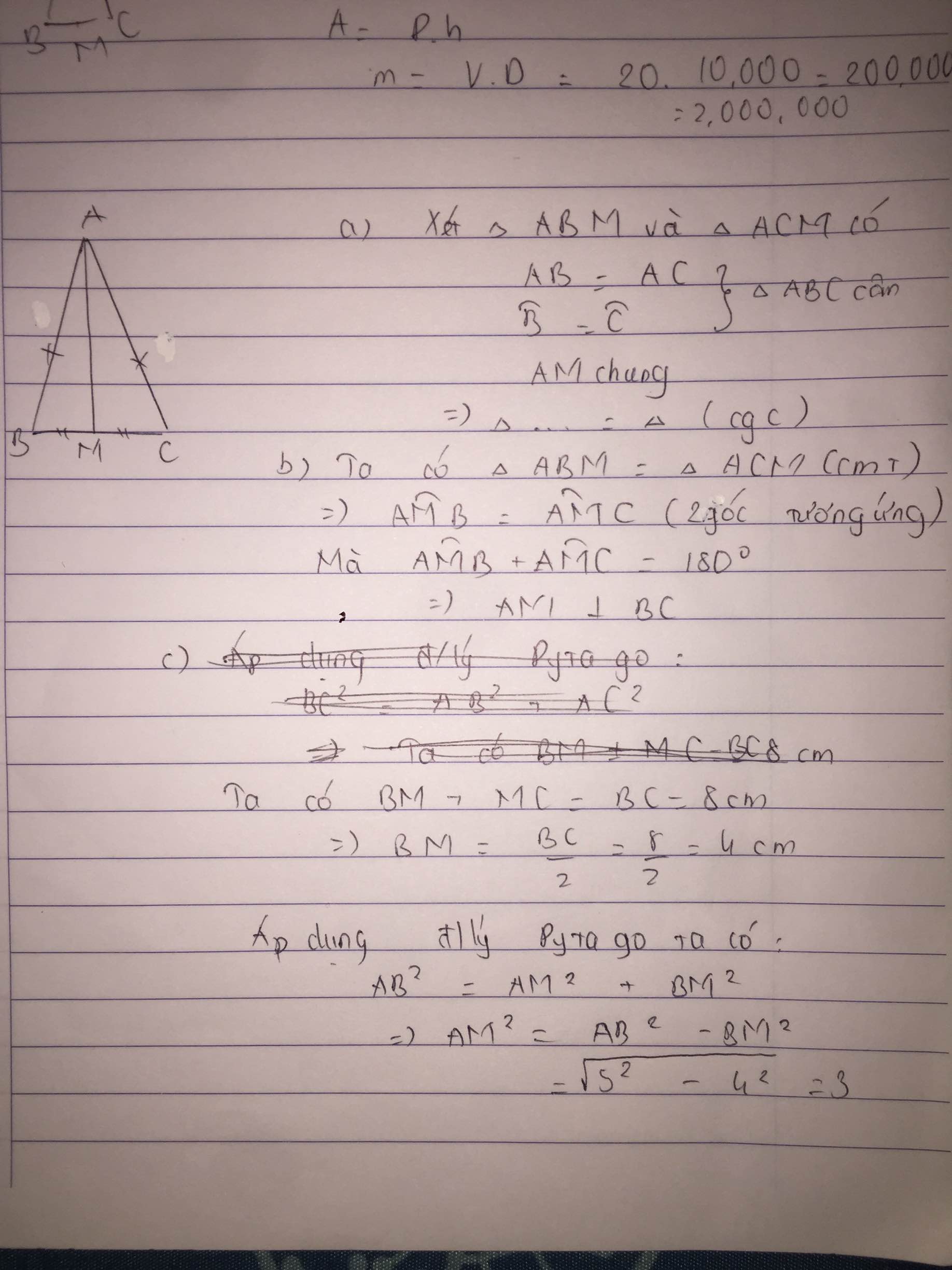

viết lại đề đi bạn :))