Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác DEF có
\(\widehat{D}+\widehat{E}+\widehat{F}=180^o\\ \Rightarrow\widehat{D}=180^o-\left(\widehat{E}+\widehat{F}\right)\\ =180^o-120^o=60^o\)
Mà
\(\widehat{E}=\widehat{F}=60^o\\ \Rightarrow\Delta DEF.cân\)

Lời giải:
Ta có : \(\Delta ABC\)là tam giác đều => \(\widehat{A}=\widehat{B}=\widehat{C}\)
Xét tam giác AFD và tam giác BED có :
AD = BE (gt)
\(\widehat{FAD}=\widehat{EBD}=60^0\)
AF = BD (gt)
=> \(\Delta AFD=\Delta BED\left(c-g-c\right)\)
=> DE = DF (hai cạnh tương ứng) (1)
Xét tam giác ADF và tam giác CEF có :
AD = CE (gt)
\(\widehat{DAF}=\widehat{ECF}=60^0\)
AF = CF (gt)
=> \(\Delta ADF=\Delta CEF\)(c-g-c)
=> DF = EF (hai cạnh tương ứng) (2)
Từ (1) và (2) => DE = DF = EF
Vậy \(\Delta DEF\)là tam giác đều

ta có góc b và e là 2 góc tương ứng góc c và f là 2 góc tương ứng suy ra chịu..........

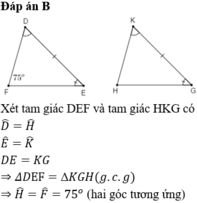

Xét tam giác DEF có
ˆD+ˆE+ˆF=180o⇒ˆD=180o−(ˆE+ˆF)=180o−120o=60oD^+E^+F^=180o⇒D^=180o−(E^+F^)=180o−120o=60o
Mà
ˆE=ˆF=60o⇒ΔDEF.cân