Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
1.
Xét tứ giác $HNMK$ có $\widehat{HNK}=\widehat{HMK}=90^0$. Mà 2 góc này cùng nhìn cạnh $HK$ nên $HNMK$ là tứ giác nội tiếp.
$\Rightarrow H,N,M,K$ cùng thuộc 1 đường tròn.
2.
Xét tứ giác $INPM$ có tổng 2 góc đối nhau $\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0$ nên $INPM$ là tứ giác nội tiếp.
$\Rightarrow I,N, P,M$ cùng thuộc 1 đường tròn.

Xét tứ giác BNMC có
\(\widehat{BNC}=\widehat{BMC}=90^0\)
=>BNMC là tứ giác nội tiếp đường tròn đường kính BC
=>BNMC nội tiếp (I)
Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=90^0+90^0=180^0\)
=>AMHN là tứ giác nội tiếp đường tròn đường kính AH
=>AMHN nội tiếp (K)
Gọi giao điểm của AH với BC là E
Xét ΔABC có
CN,BM là đường cao
CN cắt BM tại H
Do đó: H là trực tâm
=>AH vuông góc BC tại E
\(\widehat{KNH}+\widehat{INH}=\widehat{KNI}\)
\(\Leftrightarrow\widehat{KNI}=\widehat{KHN}+\widehat{NCB}\)
\(=\widehat{EHC}+\widehat{ECH}=90^0\)
\(\widehat{KMI}=\widehat{KMB}+\widehat{IMB}\)
\(=\widehat{KHM}+\widehat{MBC}\)
\(=\widehat{MBC}+\widehat{MCB}=90^0\)
Xét tứ giác KNIM có
\(\widehat{KNI}+\widehat{KMI}=180^0\)
=>KNIM nội tiếp

a: Xét tứ giác ENMF có
\(\widehat{ENF}=\widehat{EMF}\left(=90^0\right)\)
Do đó: ENMF là tứ giác nội tiếp
b: Xét tứ giác DNIM có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DNIM là tứ giác nội tiếp
a, Xét ΔENF vuông tại N
⇒ EF là đường kính của đường tròn có tâm là trung điểm của EF
Xét ΔEMF vuông tại M
⇒ EF là đường kính của đường tròn có tâm là trung điểm của EF
⇒ M,N,E,F cùng thuộc 1 đường tròn đường kính EF
b,Tương tự

a: Xét tứ giác ENMF có
\(\widehat{ENF}=\widehat{EMF}=90^0\)
Do đó: ENMF là tứ giác nội tiếp
hay E,N,M,F cùng thuộc 1 đường tròn
b: Xét tứ giác DMIN có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DMIN là tứ giác nội tiếp
hay D,M,I,N cùng thuộc 1 đường tròn

b: Xét tứ giác ANHM có
\(\widehat{ANH}+\widehat{AMH}=180^0\)
Do đó: ANHM là tứ giác nội tiếp
hay A,N,H,M cùng thuộc 1 đường tròn

Xét tứ giác DMIN có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DMIN là tứ giác nội tiếp
hay D,M,I,N cùng thuộc một đường tròn
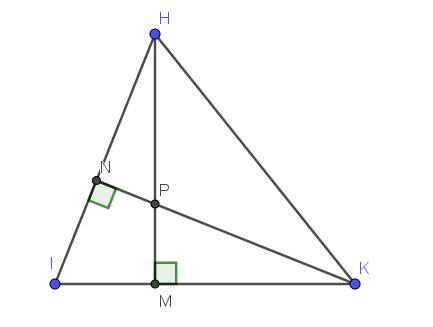
1: Xét tứ giác HNMK có
\(\widehat{HNK}=\widehat{HMK}=90^0\)
=>HNMK là tứ giác nội tiếp đường tròn đường kính HK
=>H,N,M,K cùng thuộc 1 đường tròn
2: Xét tứ giác INPM có
\(\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0\)
=>INPM là tứ giác nội tiếp
=>I,N,P,M cùng thuộc 1 đường tròn