Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình
`a)`Xét tam giác MNP cân có:MI là trung tuyến
`=>` MI là đường cao
`=>MI bot NP`
`b)` Xét tam giác vuông MIQ và tam giác vuông MIK có:
`MI` chung
`hat{NMI}=hat{PMI}`
`=>DeltaMIQ=DeltaMIK(ch-gn)`
`=>IQ=IK(1)`
`DeltaMIQ=DeltaMIK(ch-gn)`
`=>MQ=MK(2)`
`(1)(2)=>IM` là trung trực QK

a:Ta có: ΔABC cân tại A
mà AH là đường trung trực
nên AH là phân giác của góc BAC
b: Xét ΔAMI vuông tại M và ΔANI vuông tại N có
AI chung
\(\widehat{MAI}=\widehat{NAI}\)
Do đó: ΔAMI=ΔANI
Suy ra: AM=AN; IM=IN
=>AI là đường trung trực của MN
=>AH là trung trực của MN
=>HM=HN
hay ΔHMN cân tại H

a: Xét ΔNME có
ND là đường cao
ND là đường phân giác
Do đó: ΔNME cân tại N
b: Xét ΔNMD và ΔNED có
NM=NE
\(\widehat{MND}=\widehat{END}\)
ND chung
DO đó: ΔNMD=ΔNED
Suy ra: DM=DE
mà NM=NE
nên ND là đường trung trực của ME

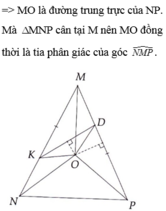

Câu a ghi sai : góc nko mới đúng
A, ta có
Tam giác mnp cân tại m
Suy ra Mn=mp
Vì mo là đường trung trực của kd nên mo vuông góc với kd ( định nghĩa)
Vì mn = mp
Kn = dp
Mà mn= mk+kn
Mp=md+dp
Suy ra mk=md ( tính chất bắc cầu)
Xét tam giác mko và tam giác mdo vuông tại o
Mk=md ( cmt)
Mo chung
Suy ra tam giác mko = tam giác mdo ( ch-cgv)
Suy ra góc mko = góc mdo
Mà góc nko + mko = 180°
Odp + mdo = 180°
Suy ra okn = góc odp . Đpcm
B, vì theo đề bài
Mo là đường trung trực của kd
Mà kd cắt đường trung trực của mp
Suy ra m thuộc đường trung trực của mp. Đpcm
C,
Theo câu a ta có
Tam giác mko = tam giác mdo
Suy ra góc kmo = góc dmo ( cạnh tương ứng)
Suy ra mo là tia phân giác của góc kmd .( định nghĩa) đpcm