Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

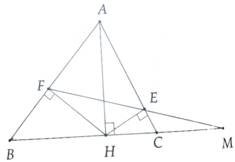
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

Gợi ý: A F E ^ = A H E ^ (tính chất hình chữ nhật và A H E ^ = A B H ^ (cùng phụ B H E ^ )

Ta có: \(\widehat{C_1}=\widehat{A_1}\)(cùng phụ với \(\widehat{B_1}\)) \(\left(1\right)\)
Xét tứ giác AEHF có: \(\widehat{A}=\widehat{E}=\widehat{F}=\widehat{H}=90^o\)
=> tứ giác AEHF là h.c.n
=> \(\widehat{A_1}=\widehat{E_1}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{E_1}=\widehat{C_1}\)
vì \(\widehat{E_1}+\widehat{BEF}=180^o\)
\(\Rightarrow\widehat{C_1}+\widehat{BEF}=180^o\) mà 2 góc đối nhau
=> tứ giác BEFC nội tiếp

b: AH^2=HB*HC
=>AH/HB=HC/HA
=>ΔAHC đồng dạng với ΔBHA
=>góc HAC=góc HBA
=>góc HAC+góc HAB=90 độ
=>góc BAC=90 độ
Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật

b: AH^2=HB*HC
=>AH/HB=HC/HA
=>ΔAHC đồng dạng với ΔBHA
=>góc HAC=góc HBA
=>góc HAC+góc HAB=90 độ
=>góc BAC=90 độ
Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)

a, Xét tam giác MNH vuông tại H, đường cao HE
\(NH^2=NE.MN\)( hệ thức lượng ) (1)
Xét tam giác NHP vuông tại H, đường cao HF
\(NH^2=NF.NP\)( hệ thức lượng ) (2)
Từ (1) ; (2) => \(NE.MN=NF.NP\)
b, Xét tam giác MNP vuông tại N, đường cao NH
\(NH^2=MH.PH\)( hệ thức lượng ) (3)
Xét tứ giác EFNH có : ^NEH = ^ENF = ^HFN = 900
=> tứ giác EFNH là hình chữ nhật => EF = NH
Ta có : \(HM.HP=FN.FP+EM.EN\)
\(\Rightarrow NH^2=HF^2+HE^2\)
Theo Pytago tam giác ENH vuông tại E : \(EH^2=NH^2-NE^2\)
Theo Pytago tam giác HNF vuông tại F : \(HF^2=HN^2-NF^2\)
\(\Rightarrow NH^2=NH^2-NE^2+HN^2-NF^2\)
Theo Pytago tam giác NEF vuông tại N : \(NE^2+NF^2=EF^2\)
\(\Rightarrow NH^2=NH^2+HN^2-\left(NE^2+NF^2\right)\)
\(=2NH^2-EF^2=2NH^2-NH^2=NH^2\)( đúng )
Vậy ta có đpcm