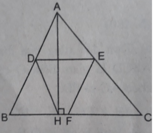
S D E C H = 22   c m 2 ;   S B D E F = 20   c m 2 ;   S D E F H = 12   c m 2

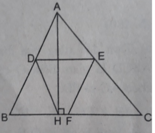
DECH là hình thang (vì có DE // CH);

BDEF là hình bình hành (vì có DE // BF và DE = BF)

DEFH là hình thang cân (vì có DE // HF và DF = HE = 1/2AC)

a: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=6\left(cm^2\right)\)

=>HA*BC=12

=>HA=2,4cm

b: Xét tứ giác AEHF có

góc AEH=góc AFH=góc FAE=90 độ

nên AEHF là hình chữ nhật

c: góc IEF=góc IEH+góc FEH

=góc IHE+góc FAH

=góc HAC+góc HCA=90 độ

=>IE vuông góc EF(1)

góc KFE=góc KFH+góc EFH

=góc KHF+góc BAH

=góc BAH+góc HBA=90 độ

=>KF vuông góc với FE(2)

Từ (1), (2) suy ra KIEF là hình thang vuông

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được: 

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay \(BC=\sqrt{100}=10cm\)

Xét ΔABC có AH là đường cao ứng với cạnh BC nên 

\(S_{ABC}=\dfrac{AH\cdot BC}{2}\)(1)

Ta có: ΔABC vuông tại A(gt)

nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}\)(2)

Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)

\(\Leftrightarrow AH\cdot10=6\cdot8=48\)

hay \(AH=\dfrac{48}{10}=4.8cm\)

Vậy: AH=4,8cm

b) Xét tứ giác AEHF có 

\(\widehat{EAF}=90^0\)(ΔABC vuông tại A, E∈AB, F∈AC)

\(\widehat{AEH}=90^0\)(HE⊥AB)

\(\widehat{AFH}=90^0\)(HF⊥AC)

Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

⇒AH=EF(Hai đường chéo của hình chữ nhật AEHF)

mà AH=4,8cm(cmt)

nên EF=4,8cm

Vậy: EF=4,8cm

a/ Xét t/g ABC có D,E lần lượt là trung điểm AB ; AC

=> DE là đường trung bình t/g ABC

=> DE // BC ; DE = BC/2

=> DE // BF ; DE = BF(do F là trung điểm BC)

=> Tứ giác BDEF là hình bình hành

b/ Có BDEF là hbh

=> EF = BD 

Xét t/g ABK vuông tại K có KD là đường trung tuyến

=> KD = 1/2 AB = BD=> EF = KD

Mà DE // BC

=> DE // KF

=> Tứ giác DEFK là htc

c/ Xét t/g AHC có ME là đường trung binh

=> ME = 1/2 HC ; ME // HC (1)

Xét t/g BHC có NF là đường trung bình

=> NF = 1/2 HC ; NF // HC (2)

(1) ; (2)

=> ME = NF ; ME // NF (3)

Xét t/g ABH có MN là đường trung bình

=> MN // AB ; MN = 1/2 ABMà

HC ⊥ AB

NF // HC=> MN ⊥ NF (4)(3) ; (4)

=> MNFE là hcn

=> NE = MF ; NE, MF cắt nhau tại trung điểm mỗi đoạn

CMTT ta có đpcm