Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔANO vuông tại N và ΔBNF vuông tại N có
NA=NB
NO=NF
=>ΔANO=ΔBNF
=>AO=BF và góc NAO=góc NBF
=>AO//BF
b: Xét tứ giác AECO có
P là trung điểm chung của AC và EO
=>AECO là hình bình hành
=>AO//CE và AO=CE; OC//AE và OC=AE
=>FB//CE và FB=CE
Xét tú giác BOCD có
M là trung điểm chung của BC và OD
=>BOCD là hình bình hành
=>BD//OC và BD=OC; OB//DC và OB=DC
=>AE//BD và AE=BD; AF//CD và AF=CD
AE=BD=CO
CD=AF=BO
BF=CE=AO
mà BO=AO=CO
nên AE=BD=CD=AF=BF=CE
=>ĐPCM

a: Xét ΔANO và ΔBNF có
NA=NB
góc ANO=góc BNF
NO=NF
=>ΔANO=ΔBNF
=>AO=BF và góc NAO=góc NBF
=>AO//BF
c: Xét ΔODE có OM/OD=OP/OE
nên MP//DE và MP=1/2DE
Xet ΔBAC có CM/CB=CP/CA=1/2
nên MP//AB và MP=1/2AB
=>DE=AB
Xét ΔODF có OM/OD=ON/OF=1/2
nên MN//FD và MN=1/2FD
Xét ΔBAC có BM/BC=BN/BA=1/2
nên MN//AC và MN=1/2AC
=>FD=AC
Xét ΔOEF có OP/OE=ON/OF=1/2
nên NP//FE và NP=1/2FE
Xét ΔABC có AN/AB=AP/AC
nên NP//BC và NP=1/2BC
=>FE=BC
=>ΔABC=ΔDEF

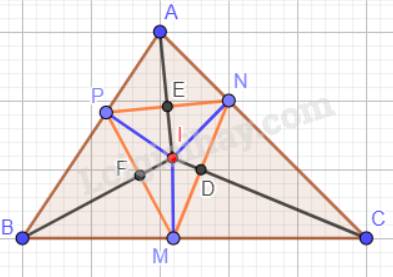
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.

Tham khảo:
Theo giả thiết ta có :
OA = OB, MA = MB ( do M là trung điểm AB )
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB
\( \Rightarrow \) MO vuông góc với AB
Theo giả thiết ta có :
OA = OC, PC = PA ( do P là trung điểm AC )
\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC
\( \Rightarrow \) PO vuông góc với AC
Theo giả thiết ta có :
OC = OB, NC = NB ( do N là trung điểm BC )
\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC
\( \Rightarrow \) NO vuông góc với BC

tự kẻ hình nha:333
a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)
xét tam giác MAB và tam giác DAB có
MH=HD(cmt)
AHM=AHD(=90 độ)
AH chung
=> tam giác MAB= tam giác DAB(cgc)
=> AM=AD( hai cạnh tương ứng)
vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)
xét tam giác AKD và tam giác AKN có
DK=NK(cmt)
AKD=AKN(=90 độ)
AK chung
=> tam giác AKD= tam giác AKN( cgc)
=> AN=AD ( hai cạnh tương ứng)
AM=AD(cmt)
=> AM=AN=> tam giác AMN cân A
b) vì E thuộc đường trung trực AB=> EM=ED
vì F thuộc đường trung trực AC=> FD=FN
ta có MN=ME+EF+FN mà EM=ED, FD=FN
=> MN= ED+EF+FD
c) xét tam giác ADF và tam giác ANF có
FD=FN(cmt)
AD=AN(cmt)
AF chung
=> tam giác ADF= tam giác ANF(ccc)
=> ANF=ADF( hai góc tương ứng)
xét tam giác AME và tam giác ADE có
AM=AD(cmt)
AE chung
EM=ED(cmt)
=> tam giác AME= tam giác ADE(ccc)
=> AME=ADE( hai góc tương ứng)
mà AME=ANF( tam giác AMN cân A)
=> ADE=ADF=> AD là p/g của EDF
d) chưa nghĩ đc :)))))))

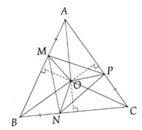
Tham khảo: