Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\triangle BEC \) vuông tại E có: \(EB^2+EC^2=BC^2\qquad (1)\) (định lý Pythagoras)
Tương tự như trên, ta có:
\(BD^2+DC^2=BC^2\qquad (2)\),
\(BD^2+DC^2=BD^2\qquad (3 )\),
\(DN^2+NC^2=DC^2\qquad(4)\),
\(EM^2+MB^2=BE^2\qquad(5)\),
\(EN^2+NC^2=EC^2\qquad(6)\).
Từ \((1)\) và \((2)\), suy ra: \(BE^2+EC^2=BD^2+DC^2(=BC^2)\).
Thay \((3)\), \((4)\), \((5)\) và \((6)\) vào đẳng thức trên, ta được:
\((ME^2+MB^2)+(EN^2+NC^2)=(DM^2+MB^2)+(DN^2+NC^2)\\ \Leftrightarrow ME^2+EN^2=MD^2+DN^2\\ \Leftrightarrow ME^2+(ED+DN)^2=(ME+ED)^2+DN^2\\ \Leftrightarrow ME^2+ED^2+2ED\cdot DN+DN^2=ME^2+2ME\cdot ED+ED^2+DN^2\\ \Leftrightarrow 2DE\cdot DN=2ME\cdot ED \Leftrightarrow DN=ME \space\text{(đpcm)}\)

a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.
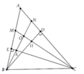

1: ΔABD vuông tại D
=>\(\widehat{ABD}+\widehat{BAD}=90^0\)
=>\(\widehat{ABD}+\widehat{BAC}=90^0\left(1\right)\)
ΔACE vuông tại E
=>\(\widehat{ACE}+\widehat{CAE}=90^0\)
=>\(\widehat{ACE}+\widehat{BAC}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{ACE}\)(3)
2: \(\widehat{ABD}+\widehat{DBC}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{ABD}=\widehat{ACE};\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{DBC}=\widehat{ECB}\)
=>\(\widehat{HBC}=\widehat{HCB}\)
=>ΔHBC cân tại H
=>HB=HC
3: BO là phân giác của góc ABD
=>\(\widehat{ABO}=\dfrac{1}{2}\cdot\widehat{ABD}\left(4\right)\)
CO là phân giác của góc ACE
=>\(\widehat{ACO}=\dfrac{1}{2}\cdot\widehat{ACE}\left(5\right)\)
Từ (3),(4),(5) suy ra \(\widehat{ABO}=\widehat{ACO}\)
\(\widehat{ABO}+\widehat{OBC}=\widehat{ABC}\)
\(\widehat{ACO}+\widehat{OCB}=\widehat{ACB}\)
mà \(\widehat{ABO}=\widehat{ACO};\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>OB=OC