
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sin R=\dfrac{PQ}{RQ}=\sin60^0=\dfrac{\sqrt{3}}{2}\Leftrightarrow PQ=\dfrac{\sqrt{3}}{2}\cdot6=3\sqrt{3}\)
Áp dụng PTG: \(PR=\sqrt{RQ^2-PQ^2}=\sqrt{36-27}=3\)

Ta có \(\sin\widehat{F}=\dfrac{ED}{EF}=\sin60^0=\dfrac{\sqrt{3}}{2}\Leftrightarrow EF=4\cdot\dfrac{2}{\sqrt{3}}=\dfrac{8\sqrt{3}}{3}\left(cm\right)\\ DF=\sqrt{EF^2-DE^2}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\left(pytago\right)\)

Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=30^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
hay \(AC=\dfrac{8\sqrt{3}}{3}\left(cm\right)\)

\(\widehat{C}=90-\widehat{B}=90-38=52\)
AC=\(\sin B.BC=\sin38.8\approx4,92cm\)
AB=\(\cos B.BC=\cos38.8\approx6,3cm\)

\(sinB=\dfrac{AC}{BC}\Rightarrow AC=sin60^0.6=3\sqrt{3}\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{6^2-\left(3\sqrt{3}\right)^2}=3\left(cm\right)\)
\(\widehat{C}=90^0-\widehat{B}=90^0-60^0=30^0\)
ΔABC vuông tại A có:
sinB=\(\dfrac{AC}{BC}=\dfrac{AC}{6}\)⇒AC=sin60.6=\(3\sqrt{3}cm\)
cosb=\(\dfrac{AB}{BC}=\dfrac{AB}{6}\)⇒AB=cos60.6=3cm
góc C = 90-góc B=90-30=60 độ

Lời giải:
$\widehat{EMH}=90^0-\widehat{MHE}=90^0-30^0=60^0$
$ME=MH\sin \widehat{MHE}=11.\sin 60^0=\frac{11\sqrt{3}}{2}$ (cm)
$EH=MH\cos \widehat{MHE}=11\cos 60^0=\frac{11}{2}$ (cm)

Bài 1:
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AB=\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{6}{7}\)
nên \(\widehat{B}=59^0\)
hay \(\widehat{C}=31^0\)

\(\widehat{B}=30^0\)
\(\Leftrightarrow AC=\dfrac{1}{2}\cdot BC\)
hay BC=16cm
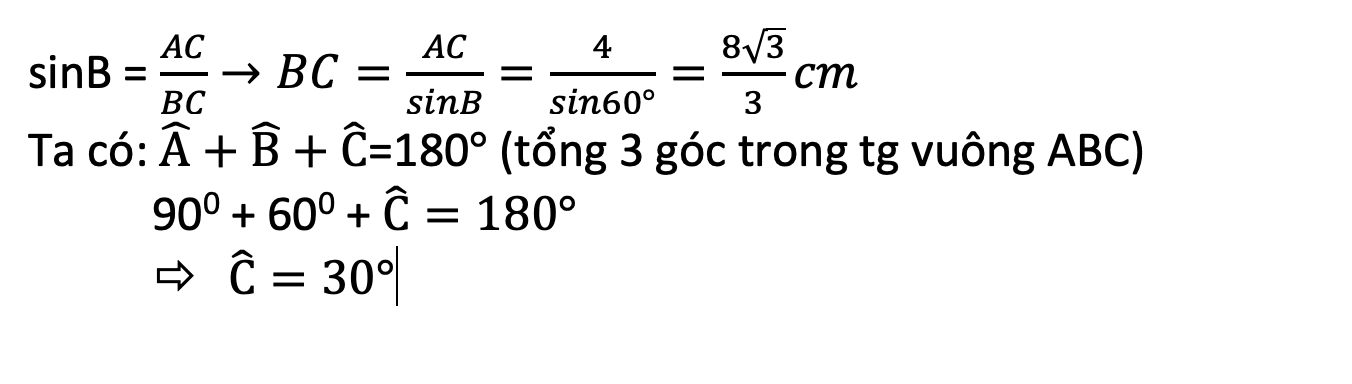

\(\sin\widehat{R}=\dfrac{QS}{RS}=\sin60^0=\dfrac{\sqrt{3}}{2}\Leftrightarrow RS=8:\dfrac{\sqrt{3}}{2}=\dfrac{16\sqrt{3}}{3}\\ QR=\sqrt{RS^2-QS^2}=\dfrac{8\sqrt{3}}{3}\left(pytago\right)\)