a. Chia các số thành 3 tập hợp:

\(A=\left\{3;6;9;12;15;18\right\}\) gồm 6 số chia hết cho 3

\(B=\left\{1;4;7;10;13;16;19\right\}\) gồm 7 số chia 3 dư 1

\(C=\left\{2;5;8;11;14;17\right\}\) gồm 6 số chia 3 dư 2

Tổng 3 số là 1 số chia hết cho 3 khi (cả 3 số đều thuộc cùng 1 tập) hoặc (3 số thuộc 3 tập khác nhau)

Số cách thỏa mãn:

\(C_6^3+C_7^3+C_6^3+C_6^1.C_7^1.C_6^1=...\)

b.

Câu b chắc người ra đề hơi rảnh rỗi?

Chia thành các tập:

\(A_1=\left\{5;10;15\right\}\) gồm 3 số chia hết cho 5

\(B_1=\left\{1;6;11;16\right\}\) 4 số chia 5 dư 1

\(C_1=\left\{2;7;12;17\right\}\) 4 số chia 5 dư 2

\(D_1=\left\{3;8;13;18\right\}\) 4 số

\(E_1=\left\{4;9;14;19\right\}\) 4 số

Tổng 3 số chia hết cho 5 khi (3 số chia hết cho 5), (1 số chia hết cho 5, 1 số dư 1, 1 số dư 4), (1 chia hết, 1 dư 2, 1 dư 3), (2 dư 1, 1 dư 3), (1 dư 1, 2 dư 2), (1 dư 2, 2 dư 4), (2 dư 3, 1 dư 4)

Số cách:

\(C_3^3+C_3^1.C_4^1.C_4^1+C_3^1.C_4^1.C_4^1+4.C_4^2.C_4^1=...\)

\(1+2+3+4+5+6=21\) chia hết cho 3

\(\Rightarrow\) Để tạo ra số có 4 chữ số chia hết cho 3 ta cần loại ra 2 chữ số có tổng chia hết cho 3

\(\Rightarrow\) 2 số đó cùng chia hết cho 3 hoặc (1 số chia 3 dư 1, 1 số chia 3 dư 2)

\(\Rightarrow\) Các cặp (3;6);(1;2);(1;5);(2;4) có 4 cặp

\(\Rightarrow\) Có 4 bộ 4 chữ số tương ứng có tổng chia hết cho 3

\(\Rightarrow4.4!=96\) số thỏa mãn

Lời giải:

Có $P_5=5!=120$ số tự nhiên có 5 chữ số được lập từ tập hợp A.

Trong tập hợp 120 số tìm được, mỗi chữ số 1,2,3,4,5 xuất hiện $\frac{120}{5}=24$ lần ở mỗi vị trí hàng chục nghìn, nghìn, trăm, chục, đơn vị.

Do đó tổng các số đó là:
$(1+2+3+4+5).24(10^4+10^3+10^2+10+1)=3999960$

Gọi : số tự nhiên có 5 chữ số có dạng: abcde 

Ta có : 

a có 5 cách chọn 

b có 4 cách chọn 

c có 3 cách chọn 

d có 2 cách chọn 

e có 1 cách chọn 

Quy tắc nhân : \(5\cdot4\cdot3\cdot2\cdot1=120\left(số\right)\)

Đáp án D

Số phần tử của tập  

Để chia hết cho 5 điều kiện cần và đủ là hay

Nếu thì lấy trong 7 chữ số 1,2,...,7 

Vậy có số tận cùng bằng 0

Nếu thì các số là số

Vây xác suất để số đó chia hết cho 5 là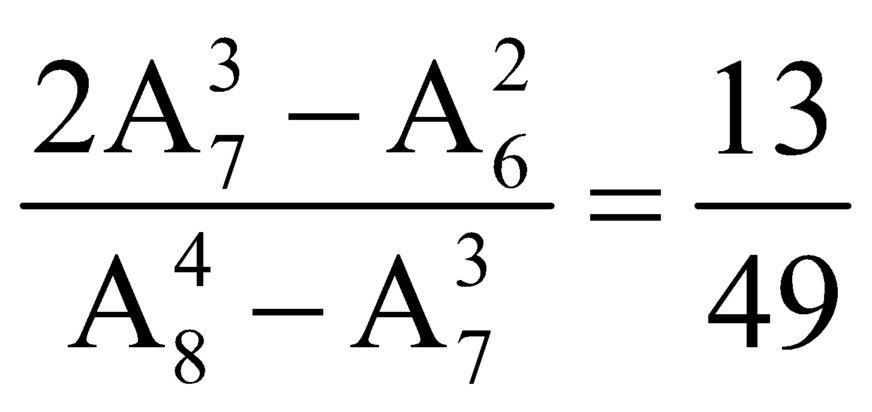  

a, số đó ko vượt quá 2147 

số đó là \(\overline{abcd}\)

vs đk trên a có 2 th 

TH1 a=1 

b có 9 cách chọn

c có 8 cách chọn

d có 7 cách chọn

TH2 a=2 

b có 2 cách chọn 

c có 3 cách chọn

d có 3 cách chọn

tổng hợp ta có 9.8.7+2.3.3=522(cách)

b, các số chia hết cho 3 { 0;3;6;9} 4 số

các số chia 3 dư 2 { 2;5;8} 3 số

các số chia 3 dư 1 {1;4;7} 3 số 

để có số có 3 chữ số chia hết cho 3 thì 3 số p cùng thuộc 1 tập hoặc mỗi số p nằm trong 1 tập

\(C_4^3+C_3^3+C_3^3+C_4^1.C_3^1.C_3^1=...\)

c, \(9.\dfrac{10!}{2!.3!}\)