a) Hiển nhiên: C, D là các tập con của \(\mathbb{R}\).

Vậy mệnh đề này đúng.

b) Mệnh đề “\(\forall x,\;x \in C \Rightarrow x \in D\)” sai. Vì \(3 \in C\) nhưng \(3 \notin D\);

c) Mệnh đề “\(3 \in C\) nhưng \(3 \notin D\)” đúng;

d) Mệnh đề “\(C = D\)” sai vì \(3 \in C\) nhưng \(3 \notin D\).

a) \(A = \{ x \in \mathbb{N}|\;x < 2\}  = \{ 0;1\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\}  = \{ 0;1\} \)

Vậy A = B, A là tập con của tập B và ngược lại.

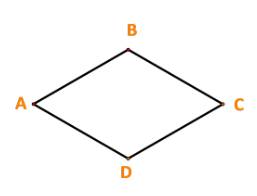
b) D là tập hợp con của C vì: Mỗi hình vuông đều là một hình thoi đặc biệt: hình thoi có một góc vuông.

\(C \ne D\) vì có nhiều hình thoi không là hình vuông, chẳng hạn:

c) \(E = ( - 1;1] = \left\{ {x \in \mathbb{R}|\; - 1 < x \le 1} \right\}\) và \(F = ( - \infty ;2] = \left\{ {x \in \mathbb{R}|\;x \le 2} \right\}\)

E là tập con của F vì \( - 1 < x \le 1 \Rightarrow x \le 2\) .

\(E \ne F\) vì \( - 3 \in F\)nhưng \( - 3 \notin E\)

a) A là tập con củ B vì:

 \( - \sqrt 3  \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3  \in B\)

\(\sqrt 3  \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3  \in B\)

Lại có: \({x^2} - 3 = 0 \Leftrightarrow x =  \pm \sqrt 3 \) nên \(B = \{  - \sqrt 3 ;\sqrt 3 \} \).

Vậy A = B.

b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.

\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.

c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.

\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)

a) Có vì \( - 1 \in B,\;1 \in B\).

b) Có vì các số tự nhiên cũng là số nguyên.

c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.

d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.

a) Mệnh đề sai, vì \(x = 0 \in \mathbb{R}\) nhưng \({0^2}\) không lớn hơn 0.

Mệnh đề phủ định của mệnh đề này là: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”

b) Mệnh đề đúng, vì \(x = 1 \in \mathbb{R}\) thỏa mãn \({1^2} = 5.1 - 4\)

Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{N},{x^2} \ne 5x - 4\)”

 c) Mệnh đề sai, vì \(2x + 1 = 0 \Leftrightarrow x =  - \frac{1}{2} \notin \mathbb{Z}\)

Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{Z},2x + 1 \ne 0\)”

a) Mệnh đề sai, vì chỉ có \(x =  - 3\) thảo mãn \(x + 3 = 0\) nhưng \( - 3 \notin \mathbb{N}\).

Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{N},x + 3 \ne 0\)”.

b) Mệnh đề đúng, vì  \({(x - 1)^2} \ge 0\) hay\({x^2} + 1 \ge 2x\) với mọi số thực x.

Mệnh đề phủ định của mệnh đề này là: “\(\exists x \in \mathbb{R},{x^2} + 1 < 2x\)”

 c) Mệnh đề sai, vì có \(a =  - 2 \in \mathbb{R},\sqrt {{{( - 2)}^2}}  = 2 \ne a\)

Mệnh đề phủ định của mệnh đề này là: “\(\exists a \in \mathbb{R},\sqrt {{a^2}}  \ne a\)”.

a) A là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 5.

\(A = \{  - 4; - 3; - 2; - 1;0;1;2;3;4\} \)

b) B là tập hợp các nghiệm thực của phương trình \(2{x^2} - x - 1 = 0.\)

\(B = \{ 1; - \frac{1}{2}\} \)

c) C là tập hợp các số tự nhiên có hai chữ số.

\(C = \{ 10;11;12;13;...;99\} \)

$X=B\backslash A=\left[-4;4\right]$.

a) Liệt kê các phần tử của tập hợp $A=\left\{x\in \mathbb{Z}|2x^2+3x+1=0\right\}$

Ta có: 2�2+3�+1=0⇔[  �=−12  �=−1 2x2+3x+1=0⇔​​  x=−21​  x=−1 ​.

Do đó: $A=\left\{-1\right\}$.

b) Cho hai tập hợp $A=\left\{x\in \mathbb{R}||x|>4\right\}$ và $B=\left\{x\in \mathbb{R}|-5\le x-1<5\right\}$. Xác định tập $X=B\backslash A$.

Ta có:

⚡$|x|>4\iff [\begin{array}{rl}& x>4\\ & x<-4\end{array}\Rightarrow A=\left(-\infty ;-4\right)\cup \left(4;+\infty \right)$.

⚡$-5\le x-1<5\iff -4\le x<6\Rightarrow B=\left[-4;6\right)$.

Suy ra $X=B\backslash A=\left[-4;4\right]$.

Ta có: \({x^2} - 6 = 0 \Leftrightarrow x =  \pm \sqrt 6  \in \mathbb{R}\)

Vì \(\sqrt 6  \in \mathbb{R}\) và \( -\sqrt 6  \in \mathbb{R}\) nên \( A = \left\{ { \pm \sqrt 6 } \right\}\)

Nhưng \( \pm \sqrt 6  \notin \mathbb{Z}\) nên không tồn tại \(x \in \mathbb{Z}\) để \({x^2} - 6 = 0\)

Hay \(B = \emptyset \).