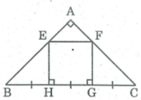
Vì ΔABC vuông cân tại A nên ∠ B =  ∠ C = 45 0

Vì ΔBHE vuông tại H có  ∠ B =  45 0  nên ΔBHE vuông cân tại H.

Suy ra HB = HE

Vì ΔCGF vuông tại G, có  ∠ C =  45 0  nên ΔCGF vuông cân tại G

Suy ra GC = GF

Ta có: BH = HG = GC (gt)

Suy ra: HE = HG = GF

Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);

Lại có  ∠ (EHG) = 90 0  nên HEFG là hình chữ nhật.

Mà EH = HG (chứng minh trên).

Vậy HEFG là hình vuông.

Tam giác vuông FGC có \(\widehat{C}=45^0\) nên là tam giác vuông cân. Do đó FG = GC

1:

ΔABC vuông cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=45^0\)

EH\(\perp\)BC tại H

=>EH\(\perp\)HB tại H

=>ΔEHB vuông tại H

Xét ΔHEB vuông tại H có \(\widehat{HBE}=45^0\)

nên ΔHEB vuông cân tại H

FG\(\perp\)BC tại G

=>FG\(\perp\)GC tại G

=>ΔFGC vuông tại G

Xét ΔFCG vuông tại G có \(\widehat{GCF}=45^0\)

nên ΔFCG vuông cân tại G

2: EH\(\perp\)BC

FG\(\perp\)BC

Do đó: EH//FG

EH=HB

HB=HG=GC

GF=GC

Do đó; EH=HB=GH=CG=GF

Xét tứ giác EHGF có

EH//FG

EH=FG

Do đó: EHFG là hình bình hành

Hình bình hành EHFG có \(\widehat{EHG}=90^0\)

nên EHFG là hình chữ nhật

Hình chữ nhật EHFG có GH=GF

nên EHFG là hình vuông

Xét tứ giác KHED có KD//EH

nên KHED là hình thang

\(\Delta\) vuông \(FGC\) có \(\widehat{C}=45^0\left(gt\right)\)

=> \(\Delta FGC\) vuông cân tại G.

=> \(FG=GC.\)

Chúc bạn học tốt!

a, Xét tam giác AHE và ABH có :

\(+,\widehat{AEH}=\widehat{AHB}=90^0\)

\(+,\widehat{HAB}chung\)

Vậy tam giác \(AHE~ABH\left(g.g\right)\)

b,

Theo hệ thức lượng trong tam giác vuông ta có :

\(AH^2=AE.AB=AF.AC\)

Vậy \(\frac{AE}{AC}=\frac{AF}{AB}\left(1\right)\)

Xét tam giác AEF và ACB có :

\(+,\)góc A chung

\(+,\left(1\right)\)

\(\Rightarrow\Delta AEF~ACB\left(c.g.c\right)\)

c, Tự làm nhé