Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

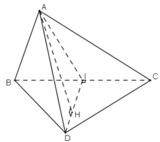
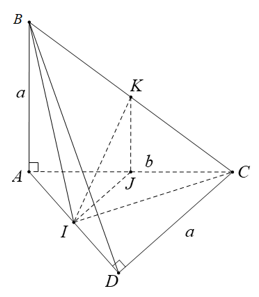
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: 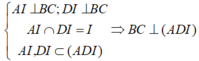
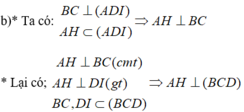

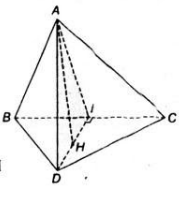
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).


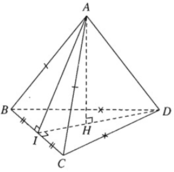
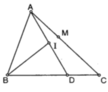
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.

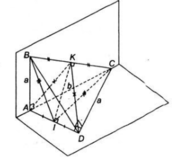


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.

A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)


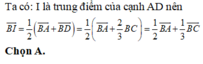


Chọn A.
+) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao: AI ⊥ BC (1)
+) Tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao: DI ⊥ BC (2)
- Từ (1) và (2) suy ra BC ⊥ (ADI).