Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
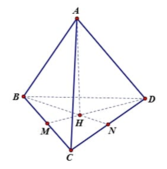
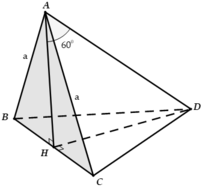
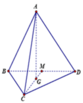
Gọi hình chiếu vuông góc hạ từ A đến mặt phẳng (BCD) là H. Khoảng cách từ A đến mặt phẳng (BCD) là AH.
Vì tứ diện đều nên H là trọng tâm tam giác BCD
⇒ B H = 2 3 . 3 a 2 = a 3 3
Trong tam giác ABH
A H = A B 2 - B H 2 = a 2 - a 2 3 = a 6 3

Tam giác A'AC vuông cân tai A và A'C=a nên A'A=AC=\(\frac{a}{\sqrt{2}}\)
Do đó : \(AB=B'C'=\frac{a}{2}\)
\(V_{ABB'C}=\frac{1}{3}B'C'.S_{\Delta ABB'}=\frac{1}{6}B'C'.AB.BB'=\frac{a^3\sqrt{2}}{48}\)
Gọi H là chân đường cao kẻ từ A của tam giác A'AB. Ta có
\(\begin{cases}AH\perp A'B\\AB\perp BC\end{cases}\)\(\Rightarrow AH\perp\left(A'BC\right)\)
Nghĩa là \(AH\perp\left(BCD'\right)\Rightarrow AH=d\left(A,\left(BCD'\right)\right)\)
Ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AA'^2}\)
Do đó \(d\left(a,\left(BCD'\right)\right)=AH=\frac{a\sqrt{6}}{6}\)

![]()
Diện tích xung quanh của hình trụ là:
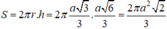
Thể tích của khối trụ là;
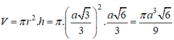

Đáp án A
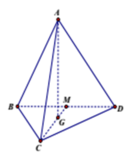
Gọi G là trọng tâm tam giác đều ABC suy ra G A ⊥ ( B C D )
Gọi M là trung điểm BD.
Đặt A C = x ⇒ G C = 2 3 C M = x 3 3
lại có A C 2 - G C 2 = A G 2
![]()
⇒ x = a 6 2

Chọn A
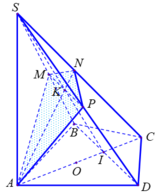
Gọi O là trọng tâm tam giác đều ABD và I là trung điểm BD thì:

Tam giác ICD vuông I có
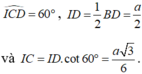
=> O và C đối xứng nhau qua đường thẳng BD

Tam giác SAC vuông tại A có SN. SC=SA²

Tam giác ABC có 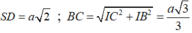 và AC²=AB²+BC²
và AC²=AB²+BC²
=> tam giác ABC vuông tại B ![]()
Lại có tam giác SAB vuông nên ![]() M là trung điểm SB
M là trung điểm SB
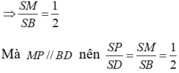
Mặt khác
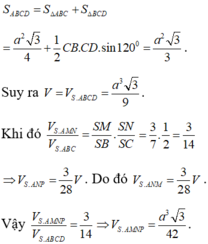




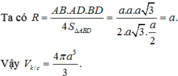


Đáp án B