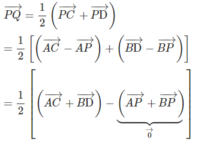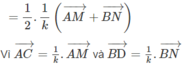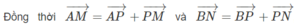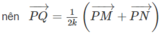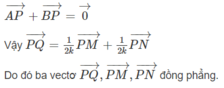Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

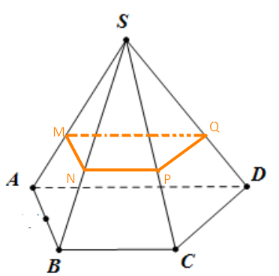
Xét tam giác SAD có: \(\dfrac{MA}{MS}=\dfrac{QD}{QS}\) suy ra MQ // AD do đó MQ // (ABCD)
Tương tự ta có: QP // (ABCD)
Vậy mp(MPQ) // mp(ABCD).
Lập luận tương tự, ta có mp(NPQ) // (ABCD).
Hai mặt phẳng (MPQ) và (NPQ) cùng đi qua điểm P và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức bốn điểm M, N, P, Q đồng phẳng.

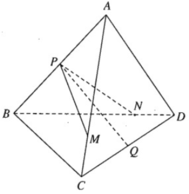
Nối NP kéo dài cắt BD tại E
Áp dụng định lý Menelaus cho tam giác CBD:
\(\frac{NC}{NB}.\frac{BE}{ED}.\frac{DP}{PC}=1\Leftrightarrow3.\frac{BE}{ED}.2=1\Rightarrow\frac{BE}{ED}=\frac{1}{6}\Rightarrow\frac{DE}{EB}=6\)
Trong mặt phẳng (ABD), nối EM kéo dài cắt AD tại Q
Áp dụng định lý Menelaus cho tam giác ABD:
\(\frac{QA}{QD}.\frac{DE}{EB}.\frac{BM}{MA}=1\Leftrightarrow\frac{QA}{QD}.6.\frac{3}{2}=1\Leftrightarrow QD=9QA\)
\(\Rightarrow k=9\)

Câu hỏi của Julian Edward - Toán lớp 11 | Học trực tuyến

Trong mp (ABD) nối PM kéo dài cắt BD tại I
Áp dụng định lý Menelaus cho tam giác ABD:
\(\dfrac{PA}{PD}.\dfrac{DI}{IB}.\dfrac{BM}{MA}=1\Leftrightarrow\dfrac{1}{3}.\dfrac{ID}{IB}.1=1\)
\(\Leftrightarrow\dfrac{ID}{IB}=3\)

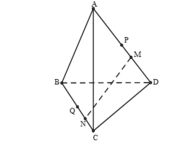
+) Do AM = 3MD; BN = 3NC suy ra:
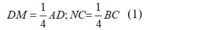
+) Do P và Q lần lượt là trung điểm của AD và BC nên :
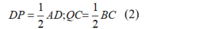
- Từ (1) và (2) suy ra: 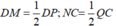
- Suy ra: M là trung điểm của DP; N là trung điểm CQ.
+) Ta có: