Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác OAB vuông cân tại O
\(\Rightarrow OM\perp AB\)
\(\Rightarrow\) cosin góc giữa 2 đường thẳng này bằng 0

Bạn tự vẽ hình nhé!
Giả sử: OC = a ⇒ OB = 3/2a và OA = 3a
Xét tam giác OAB vuông tại O có: \(AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}a\)
\(\Rightarrow AM=BM=OM=\dfrac{1}{2}AB=\dfrac{3\sqrt{5}}{4}a\)
Xét tam giác OMA, có:
\(\cos\widehat{AOM}=\dfrac{OM^2+OA^2-AM^2}{2OM.OA}=\dfrac{OA}{2OM}=\dfrac{2\sqrt{5}}{5}\)
Xét tam giác OMB, có:
\(\cos\widehat{BOM}=\dfrac{OM^2+OB^2-BM^2}{2OM.OB}=\dfrac{OB}{2OM}=\dfrac{\sqrt{5}}{4}\)
Ta có: \(\overrightarrow{OM}.\overrightarrow{AB}=\overrightarrow{OM}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)=\overrightarrow{OM}.\overrightarrow{OB}-\overrightarrow{OM}.\overrightarrow{OA}\)
\(=\dfrac{3\sqrt{5}}{4}a.\dfrac{3}{2}a.\dfrac{2\sqrt{5}}{5}-\dfrac{3\sqrt{5}}{4}a.3a.\dfrac{\sqrt{5}}{4}=\dfrac{-9}{16}a^2\)
\(\Rightarrow\cos\widehat{\left(\overrightarrow{OM},\overrightarrow{AB}\right)=\dfrac{\overrightarrow{OM}.\overrightarrow{AB}}{OM.AB}=-\dfrac{1}{10}}\)
\(\Rightarrow cos\left(OM,AB\right)=\dfrac{1}{10}\)
Hicc, ở phần tính cos BOM mình bấm máy nhầm, bạn tự bấm lại nhé. :((((
Còn cả đoạn thay cos AOM và cos BOM vào tích vô hướng cũng bị lộn giữa 2 góc á.
Kết quả ra là 3/5 nhé!
Tự dưng giờ xem lại mới nhận ra lỗi sai nghiêm trọng này. Xin lỗi bạn nhé!

Đặt \(OA=OB=2OC=2a\)
\(\Rightarrow BC=\sqrt{OB^2+OC^2}=a\sqrt{5}\) \(\Rightarrow OM=\dfrac{1}{2}BC=\dfrac{a\sqrt{5}}{2}\)
Qua B kẻ đường thẳng song song OM cắt OC kéo dài tại D
\(\Rightarrow OM\) là đường trung bình tam giác BCD \(\Rightarrow BD=2OM=a\sqrt{5}\)
\(OM||BD\Rightarrow\left(OM;AB\right)=\left(BD;AB\right)=\widehat{ABD}\)
\(AB=\sqrt{OA^2+OB^2}=2a\sqrt{2}\)
\(AD=\sqrt{OA^2+OD^2}=\sqrt{OA^2+OC^2}=a\sqrt{5}\)
\(\Rightarrow cos\widehat{ABD}=\dfrac{AB^2+BD^2-AD^2}{2AB.BD}=\dfrac{\sqrt{10}}{5}\)

\(AB=\sqrt{OA^2+OB^2}=OA\sqrt{1+k^2}\)
\(OM=BM=\dfrac{1}{2}AB=\dfrac{OA}{2}\sqrt{1+k^2}\)
\(cos\widehat{OMB}=cos60^0=\dfrac{OM^2+BM^2-OB^2}{2OM.BM}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{OA^2\left(\dfrac{k^2+1}{4}\right)+OA^2\left(\dfrac{k^2+1}{4}\right)-k^2OA^2}{2.OA^2\left(\dfrac{k^2+1}{4}\right)}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{1-k^2}{1+k^2}=\dfrac{1}{2}\Rightarrow k^2=\dfrac{1}{3}\Rightarrow k=\dfrac{1}{\sqrt{3}}\)

Gọi N là trung điểm AC \(\Rightarrow MN||AB\Rightarrow\widehat{OMN}\) là góc giữa OM và AB
Đặt \(OA=a\)
\(AB=\sqrt{OA^2+OB^2}=\sqrt{a^2+k^2a^2}=a\sqrt{k^2+1}\)
\(AC=\sqrt{OA^2+OC^2}=a\sqrt{k^2+1}\)
\(BC=\sqrt{OB^2+OC^2}=a.k\sqrt{2}\)
\(MN=\dfrac{1}{2}AB=\dfrac{a}{2}\sqrt{k^2+1}\) ; \(OM=\dfrac{BC}{2}=a.\dfrac{k\sqrt{2}}{2}\) ; \(ON=\dfrac{1}{2}AC=a.\dfrac{\sqrt{k^2+1}}{2}\)
\(cos\widehat{OMN}=cos60^0=\dfrac{OM^2+MN^2-ON^2}{2OM.MN}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{a^2.\dfrac{k^2}{2}}{2.a^2.\dfrac{k\sqrt{2k^2+2}}{4}}=\dfrac{1}{2}\Leftrightarrow2k=\sqrt{2k^2+2}\)
\(\Leftrightarrow4k^2=2k^2+2\Rightarrow k=1\)

Cau 33:
\(\left|\overrightarrow{u}-\overrightarrow{v}\right|=\sqrt{\left(\overrightarrow{u}-\overrightarrow{v}\right)^2}=\sqrt{u^2+v^2-2\cdot u\cdot v\cdot cos120}\)
\(=\sqrt{4^2+3^2-2\cdot4\cdot3\cdot\dfrac{-1}{2}}=\sqrt{37}\)
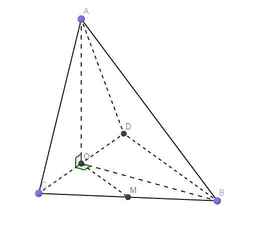
Đề bài có vấn đề gì không nhỉ?
Tam giác OAB vuông cân tại O nên OM là trung tuyến đồng thời là đường cao
\(\Rightarrow OM\perp AB\) hay góc giữa OM và AB bằng 90 độ (cosin góc giữa 2 đường thẳng bằng 0)