a) HS tự chứng minh

b) Sử dụng tổng bốn góc trong tứ giác và chú ý  B ^ = D ^

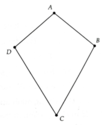
Bài 1: 

a: Ta có: AB=AD

nên A nằm trên đường trung trực của BD(1)

Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)

Từ (1) và (2) suy ra AC là đường trung trực của BD

b: Xét ΔBAC và ΔDAC có 

AB=AD

AC chung

BC=DC

Do đó: ΔBAC=ΔDAC

Suy ra: \(\widehat{B}=\widehat{D}\)

=>\(\widehat{B}=\widehat{D}=\dfrac{200^0}{2}=100^0\)

Mình lm tắt bạn tự hiểu nhé, ko hiểu chỗ nào thì hỏi mik

tam giác ADC= tam giác ABC (c.c.c)

=> A1=A2 (2 góc tg ứng)

=> AC là p/giác tam giác ADB                    (1)

Mà tam giác ABD cân do AD= AB ( giả thiết)         (2)

từ (1) và (2) => AC là trung trực tam giác ADB

=> AClà trung trực BD (đpcm)

Tự vẽ hình nha

a) Có : AB=AD(gt)

=>  A\(\in\)đường trung trực của đoạn thẳng BD(1)

   Có:  CB=CD(gt)

=> C\(\in\)đường trung trực của đoạn thẳng BD(2)

 Từ 1,2 suy ra:

          A,C \(\in\)Đường trung trực của đoạn thẳng BD

=>     AC là đường trung trực của đoạn thẳng BD

b, Xét tam giác ABC và ADC có:

        AB=AD(gt)

         BC=DC(gt)

         AC: góc chung

=> tam giác ABC=ADC( c.c.c)

=> ^BAC=^DAC(2 góc tương ứng)

     ^BCA=^DCA(2 góc tương ứng)

    ^ABC=^ADC(2 góc tương ứng)

Có: ^BAD=^BAC+^DAC=100

=> ^BAC=^DAC=50

Lại có  ^BCD=^BAC+^DCA=60

=>  ^BAC=^DCA=30

   Xét tam giác ABC có: ^BAC+^ACB+^ABC=180

                            =>   ^ABC=180- ^ACB - ^BAC=180 -60-100=20

Vậy ^B = ^C = 20

Tích mink nha (^.^)

a. Dễ thấy AEM F là hình chữ nhật => AE = FM 
Dễ thấy tg DFM vuông cân tại F => FM = DF 
=> AE = DF => tg vuông ADE = tg vuông DCF ( AE = DF; AD = DC) => DE = CF 
tg vuông ADE = tg vuông DCF => ^ADE = ^DCF => DE vuông góc CF (1) ( vì đã có AD vuông góc DC) 
b) Tương tự câu a) dễ thấy AF = BE => tg vuông ABF = tg vuông BCE => ^ABF = ^BCE => BF vuông góc CE ( vì đã có AB vuông góc BC) (2) 
Gọi H là giao điểm của BF và DE 
Từ (1) ở câu a) và (2) => H là trực tâm của tg CEF 
Mặt khác gọi N là giao điểm của BC và MF. dễ thấy CN = DF = AE: MN = EM = A F => tg vuông AEF = tg vuông CMN => ^AEF = ^MCN => CM vuông góc EF ( vì đã có CN vuông góc AE) => CM là đường cao thuộc đỉnh C của tg CE F => CM phải đi qua trực tâm H => 3 đường thẳng DE;BF,CM đồng quy tại H 
c) Dễ thấy AE + EM = AE + EB = AB = không đổi 
(AE - EM)^2 >=0 <=> AE^2 + EM^2 >= 2AE.EM <=> (AE + EM)^2 >=4AE.EM <=> [(AE + EM)/2]^2 >= AE.EM <=> AB^2/4 >=S(AEM F) 
Vậy S(AEM F ) max khi AE = EM => M trùng tâm O của hình vuông ABCD

~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~

 ~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~

~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

a. Dễ thấy AEM F là hình chữ nhật => AE = FM 
Dễ thấy tg DFM vuông cân tại F => FM = DF 
=> AE = DF => tg vuông ADE = tg vuông DCF ( AE = DF; AD = DC) => DE = CF 
tg vuông ADE = tg vuông DCF => ^ADE = ^DCF => DE vuông góc CF (1) ( vì đã có AD vuông góc DC) 
b) Tương tự câu a) dễ thấy AF = BE => tg vuông ABF = tg vuông BCE => ^ABF = ^BCE => BF vuông góc CE ( vì đã có AB vuông góc BC) (2) 
Gọi H là giao điểm của BF và DE 
Từ (1) ở câu a) và (2) => H là trực tâm của tg CEF 
Mặt khác gọi N là giao điểm của BC và MF. dễ thấy CN = DF = AE: MN = EM = A F => tg vuông AEF = tg vuông CMN => ^AEF = ^MCN => CM vuông góc EF ( vì đã có CN vuông góc AE) => CM là đường cao thuộc đỉnh C của tg CE F => CM phải đi qua trực tâm H => 3 đường thẳng DE;BF,CM đồng quy tại H 
c) Dễ thấy AE + EM = AE + EB = AB = không đổi 
(AE - EM)^2 >=0 <=> AE^2 + EM^2 >= 2AE.EM <=> (AE + EM)^2 >=4AE.EM <=> [(AE + EM)/2]^2 >= AE.EM <=> AB^2/4 >=S(AEM F) 
Vậy S(AEM F ) max khi AE = EM => M trùng tâm O của hình vuông ABCD

a) ta thấy ab = ab ; bc = cd

=> tứ giác ABCD là hình bình hành 

=> AC và BD cắt nhau tai trung điểm của mỗi đường 

=> AC là đường trung trực của BD

b) Ta có A + D = 180 

=> D = 180 - 100

=> D= 80

Ta lại có B + C = 180

=> C = 180 - 60

=> C = 120