Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) HS tự chứng minh
b) Sử dụng tổng bốn góc trong tứ giác và chú ý B ^ = D ^

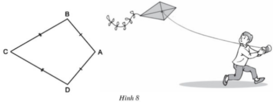
a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
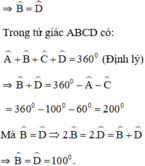

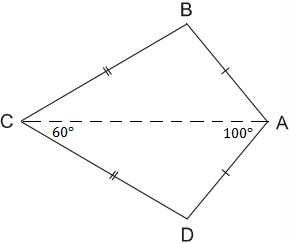
a) ta thấy ab = ab ; bc = cd
=> tứ giác ABCD là hình bình hành
=> AC và BD cắt nhau tai trung điểm của mỗi đường
=> AC là đường trung trực của BD
b) Ta có A + D = 180
=> D = 180 - 100
=> D= 80
Ta lại có B + C = 180
=> C = 180 - 60
=> C = 120

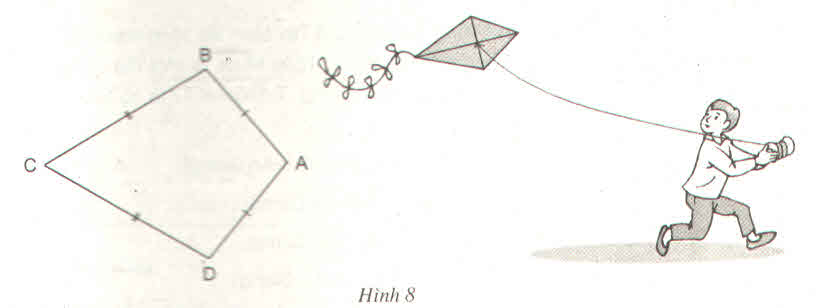
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra:
Ta có
Do đó

Tự vẽ hình nha
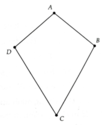
a) Có : AB=AD(gt)
=> A\(\in\)đường trung trực của đoạn thẳng BD(1)
Có: CB=CD(gt)
=> C\(\in\)đường trung trực của đoạn thẳng BD(2)
Từ 1,2 suy ra:
A,C \(\in\)Đường trung trực của đoạn thẳng BD
=> AC là đường trung trực của đoạn thẳng BD
b, Xét tam giác ABC và ADC có:
AB=AD(gt)
BC=DC(gt)
AC: góc chung
=> tam giác ABC=ADC( c.c.c)
=> ^BAC=^DAC(2 góc tương ứng)
^BCA=^DCA(2 góc tương ứng)
^ABC=^ADC(2 góc tương ứng)
Có: ^BAD=^BAC+^DAC=100
=> ^BAC=^DAC=50
Lại có ^BCD=^BAC+^DCA=60
=> ^BAC=^DCA=30
Xét tam giác ABC có: ^BAC+^ACB+^ABC=180
=> ^ABC=180- ^ACB - ^BAC=180 -60-100=20
Vậy ^B = ^C = 20
Tích mink nha (^.^)

Bài 1:
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
Ta có: CB=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
b: Xét ΔBAC và ΔDAC có
AB=AD
AC chung
BC=DC
Do đó: ΔBAC=ΔDAC
Suy ra: \(\widehat{B}=\widehat{D}\)
=>\(\widehat{B}=\widehat{D}=\dfrac{200^0}{2}=100^0\)