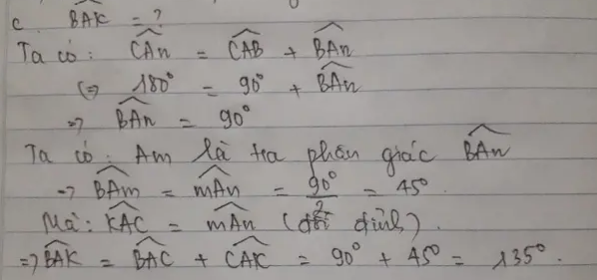Lời giải:

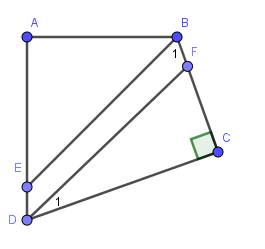
$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0$

$90^0+\widehat{B}+90^0+\widehat{D}=360^0$

$\widehat{B}+\widehat{D}=180^0$

Theo định lý tổng 3 góc trong 1 tam giác:

$\widehat{DFB}=\widehat{D_1}+\widehat{C}=\frac{1}{2}\widehat{D}+90^0$

$\Rightarrow \widehat{B_1}+\widehat{DFB}=\widehat{B_1}+\frac{1}{2}\widehat{D}+90^0$

$=\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{D}+90^0$

$=\frac{1}{2}(\widehat{B}+\widehat{D})+90^0$

$=\frac{1}{2}.180^0+90^0=180^0$

Mà 2 góc này ở vị trí trong cùng phía nên $BE\parallel DF$

Hình vẽ:

Lời giải:

$\hat{A}+\hat{B}+\hat{C}+\hat{D}=360^0$

$90^0+\hat{B}+90^0+\hat{D}=360^0$

$\hat{B}+\hat{D}=180^0$

Theo định lý tổng 3 góc trong 1 tam giác:

$\widehat{DFB}=\widehat{D^1}+\hat{C}=\genfrac{}{}{0ex}{}{1}{2}\hat{D}+90^0$

$\Rightarrow \widehat{B^1}+\widehat{DFB}=\widehat{B^1}+\genfrac{}{}{0ex}{}{1}{2}\hat{D}+90^0$

$=\genfrac{}{}{0ex}{}{1}{2}\hat{B}+\genfrac{}{}{0ex}{}{1}{2}\hat{D}+90^0$

$=\genfrac{}{}{0ex}{}{1}{2}(\hat{B}+\hat{D})+90^0$

$=\genfrac{}{}{0ex}{}{1}{2}.180^0+90^0=180^0$

Mà 2 góc này ở vị trí trong cùng phía nên $BE\parallel DF$

Ve giup minh ca hinh voi minh can cuc gap

a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)

Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o

BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o

Do đó, DAEˆ=ADEˆDAE^=ADE^

=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)

=> AE = ED (t/c tam giác cân) (đpcm)

b) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)

= DAE (câu a)

=> AD là phân giác HACˆ(đpcm)

câu tả lời

gjhjnm

mình chỉ lm dc câu a thôi 
 đặt ABx là góc ngoài tam giác ABC ( thêm x vào, dòng này ko ghi vào vở)
a)vì AD là tia phân giác của góc A, CE là tia phân giác góc C nên
      BO là tia phân giác góc B 
   => góc ABO = 1/2 góc ABC (1)
      vì BF là tia phân giác góc B nên:
     góc FBA = 1/2 góc ABx  (2)
cộng vế 1 và 2 vào ta có
     góc ABO + góc FBA = 1/2 ( góc ABC + góc ABx)
               góc FBO         =1/2  * 180 độ 
                    góc FBO    =  90 độ
=> vuông