Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

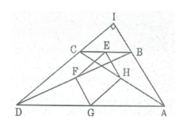
* Trong ∆ BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ∆ ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ∆ ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay ∠ (FEH) = 90 0
Vậy hình bình hành EFGH là hình chữ nhật.

+ Xét tg BCD có EF là đường trung bình => EF//=CD/2
+ Xét tg ACD có GH là đường trung bình => GH//=CD/2
=> EF//=GH => EFGH là hình bình hành (1)
+ Xét tg ABC có HE là đường trung bình => HE=AB/2 mà EF=CD/2 và AB=CD => EF=HE (2)
Từ 91) và (2) => EFGH là hình thoi => EG vuông góc với FH (2 đường chéo của hình thoi vuông góc với nhau)

Xét ΔACD có
I,G lần lượt là trung điểm của CA,CD
=>IG là đường trung bình của ΔACD
=>IG//AD và IG=AD/2(1)
Xét ΔBAD có
E,K lần lượt là trung điểm của BA,BD
=>EK là đường trung bình của ΔBAD
=>EK//AD và EK=AD/2(2)
Từ (1) và (2) suy ra EK//IG và EK=IG
Xét tứ giác EKGI có
EK//GI
EK=GI
Do đó: EKGI là hình bình hành
=>EG cắt KI tại trung điểm của mỗi đường(3)
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình của ΔABD
=>EH//BD và EH=BD/2(4)
Xét ΔCBD có
F,G lần lượt là trung điểm của CB,CD
=>FG là đường trung bình của ΔCBD
=>FG//BD và FG=BD/2(5)
Từ (4) và (5) suy ra EH//FG và EH=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
=>EG cắt HF tại trung điểm của mỗi đường(6)
Từ (3) và (6) suy ra EG,FH,IK đồng quy

Gọi I là giao điểm của hai AC và BD (1)
Ta có: AC và BD là hai đường chéo của hình chữ nhật ABCD
=> AI = IC và BI = ID
Xét tam giác ABC có: AE=EB và AI = IC
=> EI là đường trung bình của tam giác ABC
=> EG cắt AC tại I (2)
Xét tam giác ABD có AH=HD và DI=IB
=> HI là đường trung bình của tam giác ABD
=> HF cắt BD tại I (3)
Từ (1),(2),(3) suy ra EG cắt HF tại I (4)
Từ (1),(2),(3),(4) suy ra EG,HF,AC,BD đồng quy tại I

Vì HG là đường trung bình của tam giác ACD nên HG // CD. Tương tự EF là đường trung bình của tam giác BCD nên EF // CD.


Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD. Qua O kẻ các đường thẳng lần lượt vuông góc với AB,BC,CD,DA tại E,G,F,H.Chứng minh:
a) Bà điểm E,O,F thẳng hàng và ba điểm G,O,H thẳng hàng
b) Tứ giác EGFH lầ hình vuông