b: Xét tứ giác ABCD có 

AB=CD

AD=BC

Do đó: ABCD là hình bình hành

Suy ra: AB//CD;AD//BC

1/nối AC 

Do AB//CD=>BAC=ACD(so le trong)

Do AD//BC=>ACB=DAC(so le trong)

Xét ∆ABC và ∆ACD

ACB=DAC(chứng minh trên)

BAC=DAC(chứng minh trên)

AC chung

Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)

                                        AD=BC(cặp cạnh tương ứng)

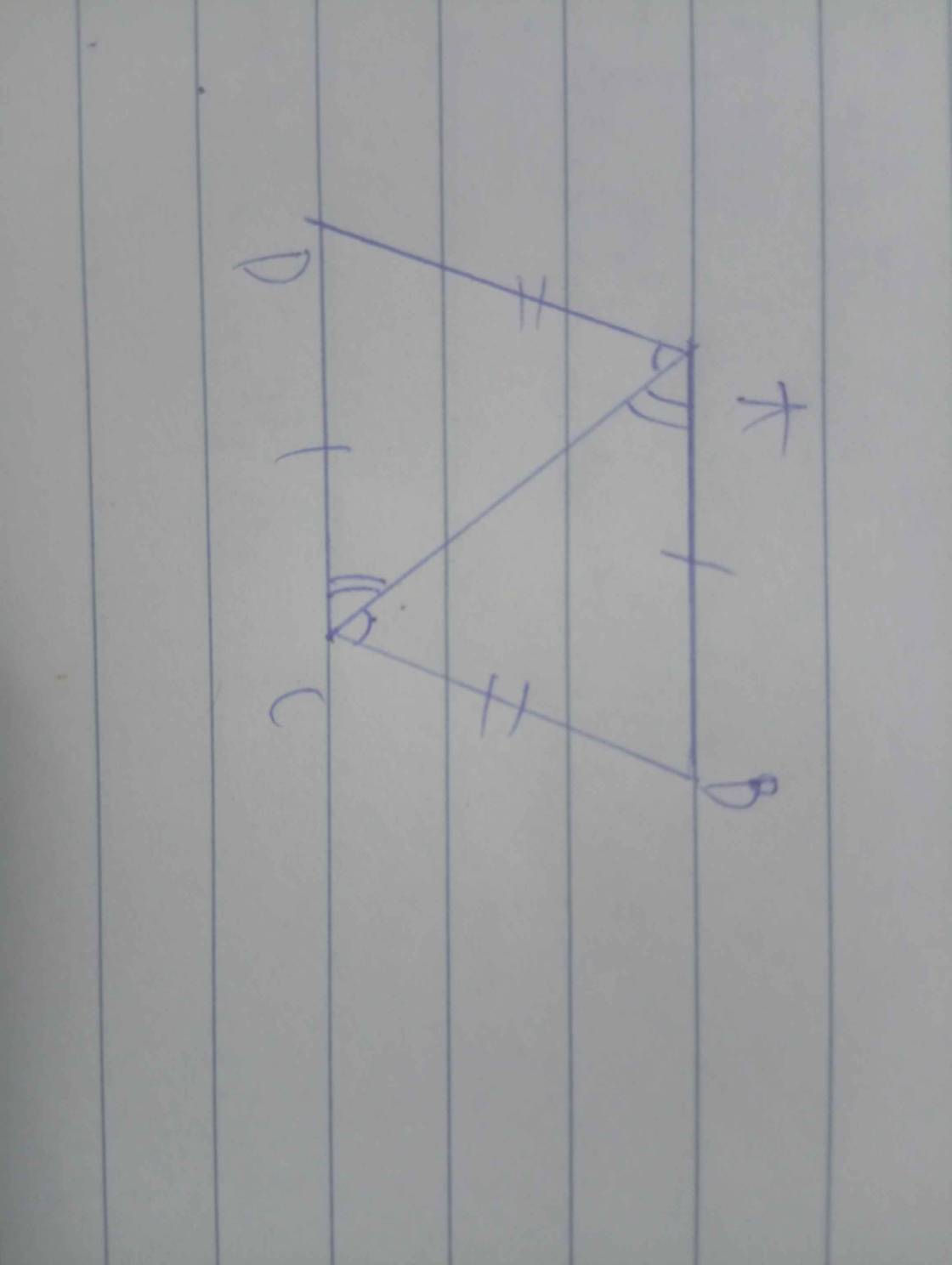
Sửa đề: góc A=góc B

a: Xét ΔDAB và ΔCBA có

DA=CB 

góc DAB=góc CBA

BA chung

=>ΔDAB=ΔCBA

b: ΔDAB=ΔCBA

=>DB=AC

b: XétΔADC và ΔBCD có

AD=BC

CD chung

AC=BD

=>ΔADC=ΔBCD

=>góc ADC=góc BCD

c: ΔADC=ΔBCD

=>góc ADC=góc BCD

góc A=góc B
góc ADC=góc BCD

=>góc BAD+góc ADC=góc ABC+góc BCD

mà góc BAD+góc ADC+góc ABC+góc BCD=360 độ

nên góc BAD+góc ADC=360/2=180 độ

=>AB//CD

Chứng minh rằng AK=KC,BI=ID 
vì FE là đường trung bình hình thang nên FE//AB//CD 
E, F là trung điểm của AD và BC nên AK=KC 
BI=ID 
( trong tam giác đường thẳng qua trung điểm của 1 cạnh, // với cạnh thứ 2 thì qua trung điểm cạnh thứ 3) 

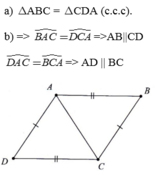
Xét t/g ABC và t/g CDA có :

AC cạnh chung

AB = CD ( gt )

\(\widehat{A1}=\widehat{C1}\)( slt , AB // CD )

\(\Rightarrow\)t/g ABC = t/g CDA ( c-g-c )

\(\Rightarrow\)BC = AD

\(\widehat{A2}=\widehat{C2}\) và 2 góc này ở vị trí slt

\(\Rightarrow\)BC // AD

1) Ta có hình vẽ sau:

Vì AB // CD nên \(\widehat{A_1}\) = \(\widehat{C_1}\) (so le trong)

AD // BC nên \(\widehat{A_2}\) = \(\widehat{C_2}\) ( so le trong)

Xét ΔABC và ΔCDA có:

\(\widehat{A_1}\) = \(\widehat{C_1}\) (cm trên)

AC: Cạnh chung

\(\widehat{A_2}\) = \(\widehat{C_2}\) (cm trên)

\(\Rightarrow\) ΔABC = ΔCDA (g.c.g) (đpcm)

2) Chứng minh tương tự ta có: ΔCDA = ABC (g.c.g)

\(\Rightarrow\) AB = CD ( 2 cạnh tương ứng) (đpcm)

3) Mình sửa lại chỗ AE = AC là AE = AB đó nha, bn ghi nhầm đề!!!

Ta có hình vẽ sau:

Xét ΔABC và ΔAFE có:

AE = AB (gt)

\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)

AF = AC (gt)

\(\Rightarrow\) ΔABC = ΔAFE(c.g.c) (đpcm)

Bạn áp dụng trường hợp bằng nhau cạnh - góc - cạnh của tam giác rồi chứng minh nha