a) tam giác AEB vuông tại E có EH là đường cao \(\Rightarrow BH.BA=BE^2\)

tam giác CEB vuông tại E có EK là đường cao \(\Rightarrow BK.BC=BE^2\)

\(\Rightarrow BH.BA=BK.BC\)

b) \(BH.BA=BK.BC\Rightarrow\dfrac{BH}{BC}=\dfrac{BK}{BA}\)

Xét \(\Delta BHK\) và \(\Delta BCA:\) Ta có: \(\left\{{}\begin{matrix}\angle ABCchung\\\dfrac{BH}{BC}=\dfrac{BK}{BA}\end{matrix}\right.\)

\(\Rightarrow\Delta BHK\sim\Delta BCA\left(c-g-c\right)\)

b) \(\Delta BHK\sim\Delta BCA\Rightarrow\angle BHK=\angle BCA\)

Kẻ \(ED\bot CF\) 

Vì \(\angle EHF=\angle EDF=\angle HFD=90\Rightarrow EHFD\) là hình chữ nhật

\(\Rightarrow HD\) và EF cắt nhau tại trung điểm I của mỗi đường

Vì \(\Delta EHF\) vuông tại H có I là trung điểm EF 

\(\Rightarrow\angle FHI=\angle HFI=\angle AFE\left(1\right)\)

Xét \(\Delta AFC\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AFC=\angle AEB=90\end{matrix}\right.\)

\(\Rightarrow\Delta AFC\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)

Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AF}{AC}=\dfrac{AE}{AB}\end{matrix}\right.\)

\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\Rightarrow\angle AFE=\angle ACB\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\angle FHI=\angle ACB=\angle BHK\Rightarrow\angle BHD=BHK\)

\(\Rightarrow H,D,K\) thẳng hàng \(\Rightarrow H,I,K\) thẳng hàng

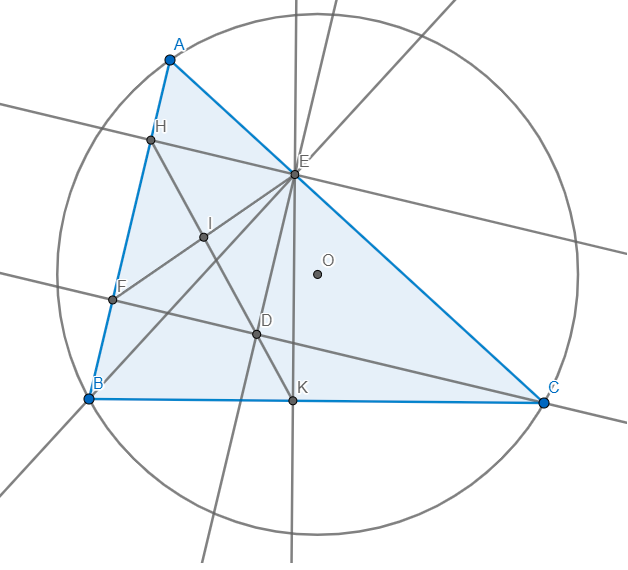
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEA vuông tại E có EH là đường cao ứng với cạnh huyền AB, ta được:

\(BH\cdot BA=BE^2\)(1)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEC vuông tại E có EK là đường cao ứng với cạnh huyền AC, ta được:

\(BK\cdot BC=BE^2\)(2)

Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)

b) Xét ΔBHK và ΔBCA có 

\(\dfrac{BH}{BC}=\dfrac{BK}{BA}\)(cmt)

\(\widehat{HBK}\) chung

Do đó: ΔBHK\(\sim\)ΔBCA(c-g-c)

Câu 1: 

a: Xét ΔAHB vuông tạiH có HD là đường cao

nên \(AD\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HE là đường cao

nên \(AE\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)

\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)

\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

b: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB

nên \(AE\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC

nên \(AF\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)