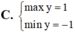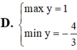Chọn D

a.

TXĐ: \(D=\left[-4;2\right]\)

\(0\le\sqrt{9-\left(x+1\right)^2}\le3\Rightarrow-1\le\sqrt{9-\left(x+1\right)^2}\le2\)

\(\Rightarrow f'\left(\sqrt{8-x^2-2x}-1\right)\le0\) ; \(\forall x\in D\)

\(g'\left(x\right)=-\dfrac{x+1}{\sqrt{8-x^2-2x}}.f'\left(\sqrt{8-x^2-2x}-1\right)\) luôn cùng dấu \(x+1\)

\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[-1;2\right]\) và nghịch biến trên \(\left[-4;-1\right]\)

Từ BBT ta thấy \(g\left(x\right)_{max}=g\left(-4\right)=g\left(2\right)=f\left(-1\right)=?\)

\(g\left(x\right)_{min}=g\left(-1\right)=f\left(2\right)=?\)

(Do đề chỉ có thế này nên ko thể xác định cụ thể được min-max)

b.

\(g'\left(x\right)=\left(2x+1\right).f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\f'\left(x^2+x\right)=0\left(1\right)\end{matrix}\right.\)

Xét (1), ta chỉ cần quan tâm 2 nghiệm bội lẻ:

\(f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x^2+x=-1\left(vô-nghiệm\right)\\x^2+x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Với \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\) \(\Rightarrow x^2+x\ge2\) ; với \(-2\le x\le1\Rightarrow-1\le x^2+x\le2\) nên ta có bảng xét dấu:

Từ BBT ta có: \(x=-\dfrac{1}{2}\) là cực đại, \(x=-2;x=1\) là 2 cực tiểu

Hàm đồng biến trên ... bạn tự kết luận

Bài 1:

Đặt \(\left\{\begin{matrix} x+y=a\\ xy=b\end{matrix}\right.\Rightarrow x^2+y^2+xy=a^2-b=3\)

Vì \(x,y\geq 0\rightarrow b\geq 0\rightarrow a^2=3+b\geq 3\)

Biến đổi:

\(T=(x+y)^3-3xy(x+y)-[(x+y)^2-2xy]\)

\(\Leftrightarrow T=a^3-3ab-a^2+2b\)

\(\Leftrightarrow T=a^3-3a(a^2-3)-a^2+2(a^2-3)=-2a^3+a^2+9a-6\)

Xét đạo hàm và lập bảng biến thiên hàm trên với điều kiện \(a\geq \sqrt{3}\) ta thu được \(T_{\max}=3\sqrt{3}-3\Leftrightarrow a=\sqrt{3}\Leftrightarrow (x,y)=(\sqrt{3},0)\)

Hàm không có min.

Chọn B

Chọn A

Hàm số y = f(x) =  2 x + m x - 1 . xác định và liên tục trên [2;3].

Với m = -2, hàm số trở thành y = 2(không thỏa)

Với  ta có: 

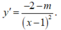
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]

Suy ra 

Do đó: 

Theo giả thiết 

Vậy tổng các giá trị của tham số  thỏa mãn yêu cầu bài toán là: -4.

Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức  là không cần thiết.

Chọn A

Hàm số y = f(x) =  2 x + m x - 1 xác định và liên tục trên [2;3]

 Với m = -2, hàm số trở thành y = 2  (không thỏa).

Với m ≠ 2, ta có: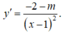 

Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]

Suy ra 

Do đó: 

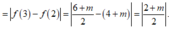
Theo giả thiết 

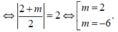
Vậy tổng các giá trị của tham số  thỏa mãn yêu cầu bài toán là: -4.

Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức   là không cần thiết.