
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Q
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
Q
1

13 tháng 6 2018
\(a^4+b^4+c^4=\left(a^2+b^2+c^2\right)^2-2abc\left(a+b+c\right)\)
thay \(\hept{\begin{cases}a+b+c=0\\a^2+b^2+c^2=0\end{cases}}\)
=>\(a^4+b^4+c^4=14^2-2abc.0=196\)
NP
0

PT
1
MD
1

ND
7 tháng 4 2018
THam khảo tại đây:
Câu hỏi của Vũ khoa - Toán lớp 8 - Học toán với OnlineMath
ND
1

C
31 tháng 10 2019
Ta có: \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0\)
\(\Rightarrow\frac{ayz+bxz+cxy}{xyz}=0\)
\(\Rightarrow ayz+bxz+cxy=0\)
Lại có: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2.\frac{ayz+bxz+cxy}{abc}=1\)(bình phương hai vế)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)(Vì \(ayz+bxz+cxy=0\))
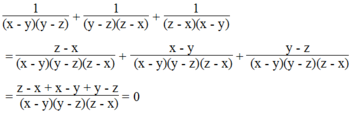
\(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=\frac{ayz+bxz+cxy}{xyz}=0\Rightarrow ayz+bxz+cxy=0\)
\(\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{xy}{ab}+\frac{xz}{ac}+\frac{yz}{bc}\right)\)
\(=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{cxy+bxz+ayz}{abc}\right)=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\cdot\frac{0}{abc}=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2\)mà \(\left(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\right)^2=1^2=1\)
\(\Rightarrow\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)