cảm ơn nha^-^

a: \(\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}\)

\(=\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{DA}+\overrightarrow{AD}\)

\(=\overrightarrow{0}\)

câu a phải là CM \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\) chứ nhỉ?

a/ \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)

\(=\overrightarrow{AD}+\overrightarrow{CB}\)

b/ \(\overrightarrow{AB}=\overrightarrow{CD}\Leftrightarrow\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{CB}+\overrightarrow{BD}\)

\(\Leftrightarrow\overrightarrow{AC}=\overrightarrow{BD}\)

Câu c nghe nó sai sai kiểu j ấy, \(\overrightarrow{AB},\overrightarrow{AC}\) tạo thành \(\widehat{BAC}\) rồi thì làm sao thành phân giác đc :))

đúng rồi câu c bị lag :v

a) Đúng

Giải thích: Nhận thấy a→ = -3.i→

Vì –3 < 0 nên a→ và i→ ngược hướng.

b) Đúng.

Giải thích:

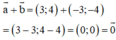
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.

c) Sai

Giải thích:

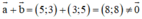
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.

d) Đúng

Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

cảm ơn nha ^-^

Lời giải:
Vì $O$ là tâm hình bình hành nên $O$ là trung điểm của $AC, BD$

$\Rightarrow \overrightarrow{OA}, \overrightarrow{OC}; \overrightarrow{OB}, \overrightarrow{OD}$ là 2 cặp vecto đối nhau

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$ (đpcm)

b) Theo phần a ta có:

\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OC}\)

\(=\overrightarrow{MO}+\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{MO}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{OD}\)

\(=(\overrightarrow{MO}+\overrightarrow{OB})+(\overrightarrow{MO}+\overrightarrow{OD})=\overrightarrow{MB}+\overrightarrow{MD}\) (đpcm)

Hình vẽ: