Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,x^3+6x^2y+12xy^2+8y^3\\ =x^3+3.2x^2+3.2^2.x+\left(2y\right)^3\\ =\left(x+2y\right)^3\)
\(b,x^3-3x^2+3x-1\\ =x^3-3x^2.1+3x.1^2-1^3\\ =\left(x-1\right)^3\)
a) \(x^3+6x^2y+12xy^2+8y^3\)
\(=x^3+3\cdot x^2\cdot2y+2\cdot x\cdot\left(2y\right)^2+\left(2y\right)^3\)
\(=\left(x+2y\right)^3\)
b) \(x^3-3x^2+3x-1\)
\(=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3\)
\(=\left(x-1\right)^3\)

2:
-8x^6-12x^4y-6x^2y^2-y^3
=-(8x^6+12x^4y+6x^2y^2+y^3)
=-(2x^2+y)^3
3:
=(1/3)^2-(2x-y)^2
=(1/3-2x+y)(1/3+2x-y)

HĐT số 4: \(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
__________
\(x^3+3x^2+3x+1\)
\(=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\)
\(=\left(x+1\right)^3\)


Ta có x 3 – 6 x 2 + 12 x – 8 = x 3 – 3 . x 2 . 2 + 3 . x . 2 2 – 2 3 = ( x – 2 ) 3
Đáp án cần chọn là: D

Ta có : x 3 - 6 x 2 y + 12 x y 2 - 8 y 3 = ( x ) 3 - 3 . x 2 . 2 y + 3 . x . ( 2 y ) 2 - ( 2 y ) 3 = ( x - 2 y ) 3

Ta có
8 x 3 – 12 x 2 y + 6 x y 2 – y 3 = ( 2 x ) 3 – 3 . ( 2 x ) 2 y + 3 . 2 x . y 2 – y 3 = ( 2 x – y ) 3
Đáp án cần chọn là: A
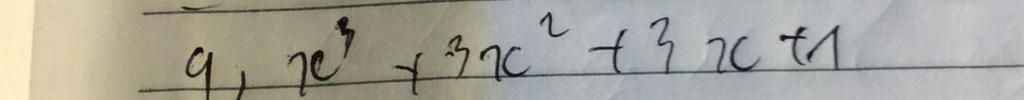
Mình khẳng định điều ngược lại:
"Không thể biểu diễn lập phương 1 số nguyên dưới dạng hiệu lập phương 2 số nguyên"
Tức là không tồn tại nghiệm nguyên a;b;c của :
a3 = c3 - b3 hay cũng tương đương a3 + b3 = c3
Lời giải ở đây.
math.stanford.edu/~lekheng/flt/wiles.pdf