Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x2 - 2x + 3 = ( x2 - 2x + 1 ) + 2 = ( x - 1 )2 + 2 ≥ 2 > 0 ∀ x ( đpcm )
x2 - x + 1 = ( x2 - x + 1/4 ) + 3/4 = ( x - 1/2 )2 + 3/4 ≥ 3/4 > 0 ∀ x ( đpcm )
x2 + 4x + 7 = ( x2 + 4x + 4 ) + 3 = ( x + 2 )2 + 3 ≥ 3 > 0 ∀ x ( đpcm )
-x2 + 4x - 5 = -( x2 - 4x + 4 ) - 1 = -( x - 2 )2 - 1 ≤ -1 < 0 ∀ x ( đpcm )
-x2 - x - 1 = -( x2 + x + 1/4 ) - 3/4 = -( x + 1/2 )2 - 3/4 ≤ -3/4 < 0 ∀ x ( đpcm )
-4x2 - 4x - 2 = -4( x2 + x + 1/4 ) - 1 = -4( x + 1/2 )2 - 1 ≤ -1 < 0 ∀ x ( đpcm )

a, Ta co : A = 1999 * 2001
= ( 2000 - 1 ) *( 2000 + 1 )
= \(2000^2-1\)
Vây A < B
cậu ơi tối mình về mình làm tiếp cho bây giờ mình phải đi hok .

Bài 1 : Chứng minh phương trình vô nghiệm :
a, Ta có : \(x+2=x+5\)
=> \(x+2-x-5=0\)
=> \(-3=0\left(VL\right)\)
Vậy phương trình vô nghiệm .
b, Ta có : \(x^2-x+1=0\)
=> \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\) ( Vô lý )
Vậy phương trình vô nghiệm .

2) \(x^4-x^2+1=0\)(1)
Đặt: t=x2, khi đó:
(1)\(\Leftrightarrow t^2-t+1=0\)
\(\Leftrightarrow\left(t-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(2\right)\)
\(\Rightarrow\left(2\right)\) vô nghiệm => (1) vô nghiệm

Bài 1:
a) Ta có: \(VT=\frac{-u^2+3u-2}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(u^2-3u+2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(n^2-u-2u+2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left[u\left(u-1\right)-2\left(u-1\right)\right]}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(u-1\right)\left(u-2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{2-u}{u+2}\)(1)
Ta có: \(VP=\frac{u^2-4u+4}{4-u^2}\)
\(=\frac{\left(u-2\right)^2}{-\left(u-2\right)\left(u+2\right)}\)
\(=\frac{-\left(u-2\right)}{u+2}\)
\(=\frac{2-u}{u+2}\)(2)
Từ (1) và (2) suy ra \(\frac{-u^2+3u-2}{\left(u+2\right)\left(u-1\right)}=\frac{u^2-4u+4}{4-u^2}\)
b) Ta có: \(VT=\frac{v^3+27}{v^2-3v+9}\)
\(=\frac{\left(v+3\right)\left(v^3-3u+9\right)}{v^2-3u+9}\)
\(=v+3=VP\)(đpcm)
Bài 2:
a) Ta có: \(\frac{3x^2-2x-5}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{3x^2-5x+3x-5}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{x\left(3x-5\right)+\left(3x-5\right)}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{\left(3x-5\right)\left(x+1\right)}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow M=\frac{\left(3x-5\right)\left(x+1\right)\left(2x-3\right)}{3x-5}\)
\(\Leftrightarrow M=\left(x+1\right)\left(2x-3\right)\)
\(\Leftrightarrow M=2x^2-3x+2x-3\)
hay \(M=2x^2-x-3\)
Vậy: \(M=2x^2-x-3\)
b) Ta có: \(\frac{2x^2+3x-2}{x^2-4}=\frac{M}{x^2-4x+4}\)
\(\Leftrightarrow\frac{2x^2+4x-x-2}{\left(x-2\right)\left(x+2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{2x\left(x+2\right)-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{\left(x+2\right)\left(2x-1\right)}{\left(x+2\right)\left(x-2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{M}{\left(x-2\right)^2}=\frac{2x-1}{x-2}\)
\(\Leftrightarrow M=\frac{\left(2x-1\right)\left(x-2\right)^2}{\left(x-2\right)}\)
\(\Leftrightarrow M=\left(2x-1\right)\left(x-2\right)\)
\(\Leftrightarrow M=2x^2-4x-x+2\)
hay \(M=2x^2-5x+2\)
Vậy: \(M=2x^2-5x+2\)
Bài 3:
a) Ta có: \(\frac{x+1}{N}=\frac{x^2-2x+4}{x^3+8}\)
\(\Leftrightarrow\frac{x+1}{N}=\frac{x^2-2x+4}{\left(x+2\right)\left(x^2-2x+4\right)}\)
\(\Leftrightarrow\frac{x+1}{N}=\frac{1}{x+2}\)
\(\Leftrightarrow N=\left(x+1\right)\left(x+2\right)\)
hay \(N=x^2+3x+2\)
Vậy: \(N=x^2+3x+2\)
n) Ta có: \(\frac{\left(x-3\right)\cdot N}{3+x}=\frac{2x^3-8x^2-6x+36}{2+x}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=\frac{2x^3+4x^2-12x^2-24x+18x+36}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{\left(x+3\right)}=\frac{2x^2\left(x+2\right)-12x\left(x+2\right)+18\left(x+2\right)}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=\frac{\left(x+2\right)\left(2x^2-12x+18\right)}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=2x^2-12x+18\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=2x^2-6x-6x+18=2x\left(x-3\right)-6\left(x-3\right)=2\cdot\left(x-3\right)^2\)
\(\Leftrightarrow N\cdot\left(x-3\right)=\frac{2\left(x-3\right)^2}{x+3}\)
\(\Leftrightarrow N=\frac{2\left(x-3\right)^2}{x+3}:\left(x-3\right)=\frac{2\left(x-3\right)^2}{\left(x+3\right)\left(x-3\right)}\)
\(\Leftrightarrow N=\frac{2\left(x-3\right)}{x+3}\)
hay \(N=\frac{2x-6}{x+3}\)
Vậy: \(N=\frac{2x-6}{x+3}\)
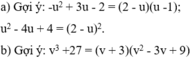
Biến đổi vế trái chúng ta thu được vế phải.