
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số đo góc ngoài tại đỉnh D là:
\(180^0-360^0+70^0+90^0+120^0=100^0\)

a) Ta có: \(2x+x^2=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
b) Ta có: \(\left(2x+1\right)^2-25=0\)
\(\Leftrightarrow\left(2x-4\right)\left(2x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

a) \(5x+10y=5\left(x+2y\right)\)
b) \(3x^2y+9xy^2z=3xy\left(x+3yz\right)\)
g) \(x^2-x-6=\left(x-3\right)\left(x+2\right)\)
h) \(x^2+9x+8=\left(x+8\right)\left(x+1\right)\)
l) \(x^2-10x+9=\left(x-1\right)\left(x-9\right)\)
k) \(x^2+x-12=\left(x+4\right)\left(x-3\right)\)
l) \(3x^2+8x+4=\left(3x+2\right)\left(x+2\right)\)

\(a,\left(2x+3\right).5x=10x^2.15x\)
\(b,1011^2-1010^2=\left(1011-1010\right)\left(1011+1010\right)=2021\)
\(c,x^2+3x=x\left(x+3\right)\)
\(c,x^2+2xy-x-2y=\left(x^2-x\right)+\left(2xy-2y\right)=x\left(x-1\right)+2y\left(x-1\right)=\left(x-1\right)\left(x+2y\right)\)

b: Ta có: \(5x\left(12x+7\right)-3x\left(20x-5\right)=-100\)
\(\Leftrightarrow60x^2+35x-60x^2+15x=-100\)
\(\Leftrightarrow50x=-100\)
hay x=-2

a: Ta có: \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2\)
\(=x^3-1-x^3+2\)
=1
b: ta có: \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5\)
\(=8x^3-y^3-8x^3-5\)
\(=-y^3-5\)
c: Ta có: \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2\)
\(=x^3+1-x^3+2\)
=3
d: Ta có: \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5\)
\(=8x^3+y^3-8x^3-5\)
\(=y^3-5\)
a) \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2=x^3-1-x^3+2=1\)
b) \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5=8x^3-y^3-8x^3-5=-y^3-5\)
c) \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2=x^2+1-x^3+2=3\)
d) \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5=8x^3+y^3-8x^3-5=y^3-5\)
e) \(\left(3x+2\right)\left(9x^2-6x+4\right)-27x^3-7=27x^3+8-27x^3-7=1\)
f) \(\left(3x-2\right)\left(9x^2+6x+4\right)-27x^3-7=27x^3-8-27x^3-7=-15\)


1: BC=căn 7,5^2+10^2=12,5cm
AH=7,5*10/12,5=6cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hcn
=>DE=AH=6cm
2: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HElà đường cao
nên AE*AC=AH^2
=>AD*AB=AE*AC
3: ΔAHB vuông tại H có HD là đường cao
nên DH^2=AD*DB
4: AD=AH^2/AB=6^2/7,5=36/7,5=4,8cm
AE=AH^2/AC=6^2/10=3,6cm
S AED=1/2*3,6*4,8=8,64cm2


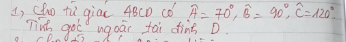 giúp, mình vs ạ, mình cảm tạ ạ
giúp, mình vs ạ, mình cảm tạ ạ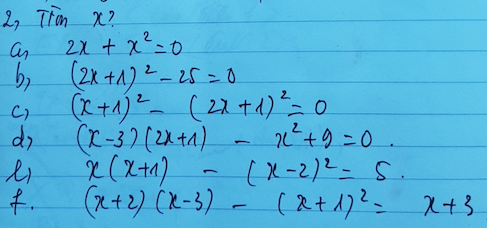
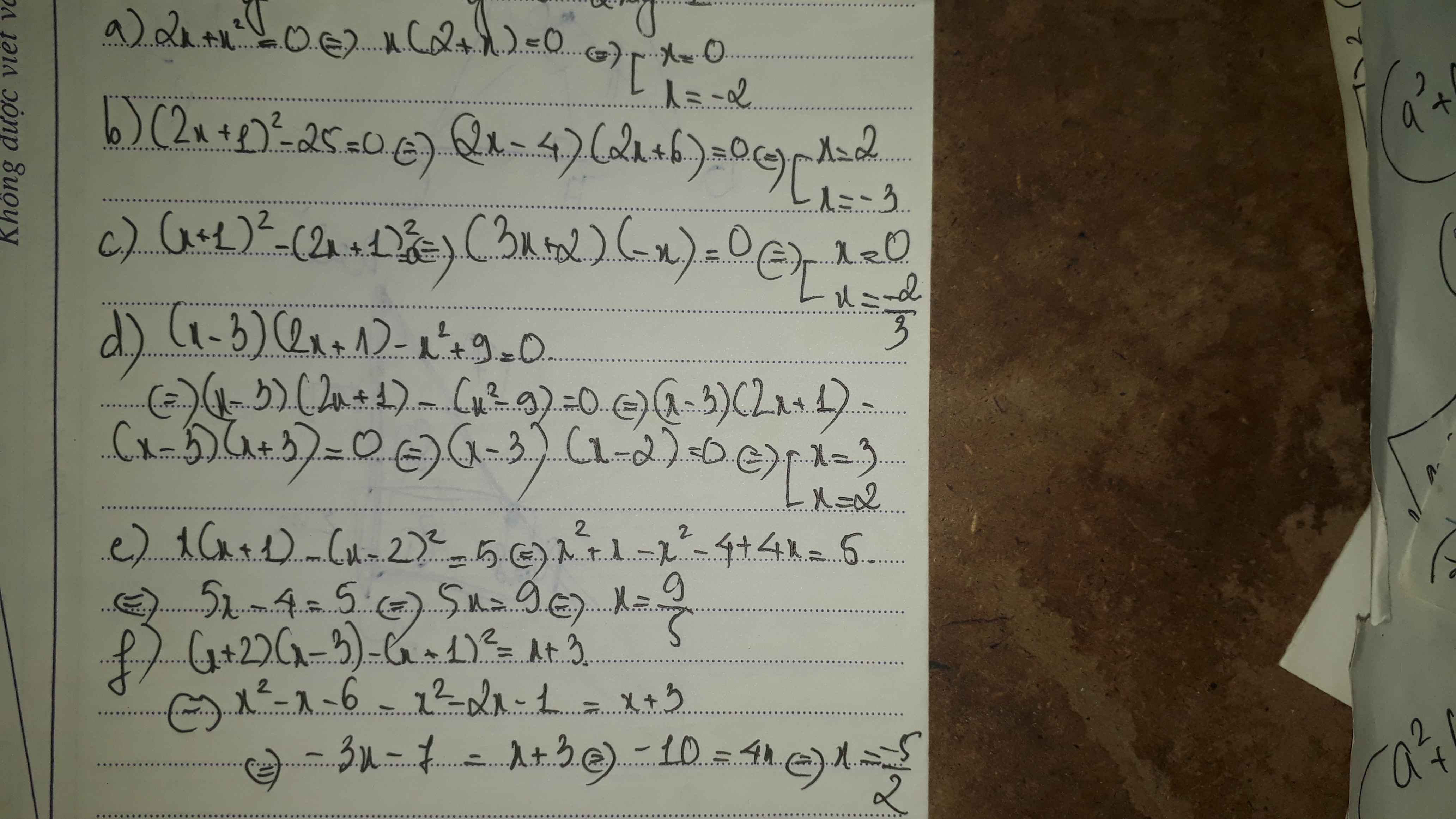
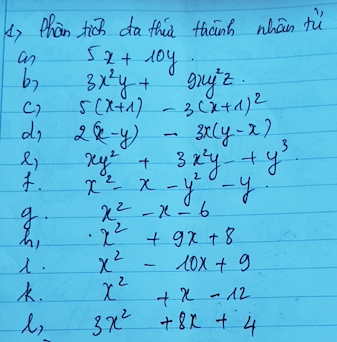

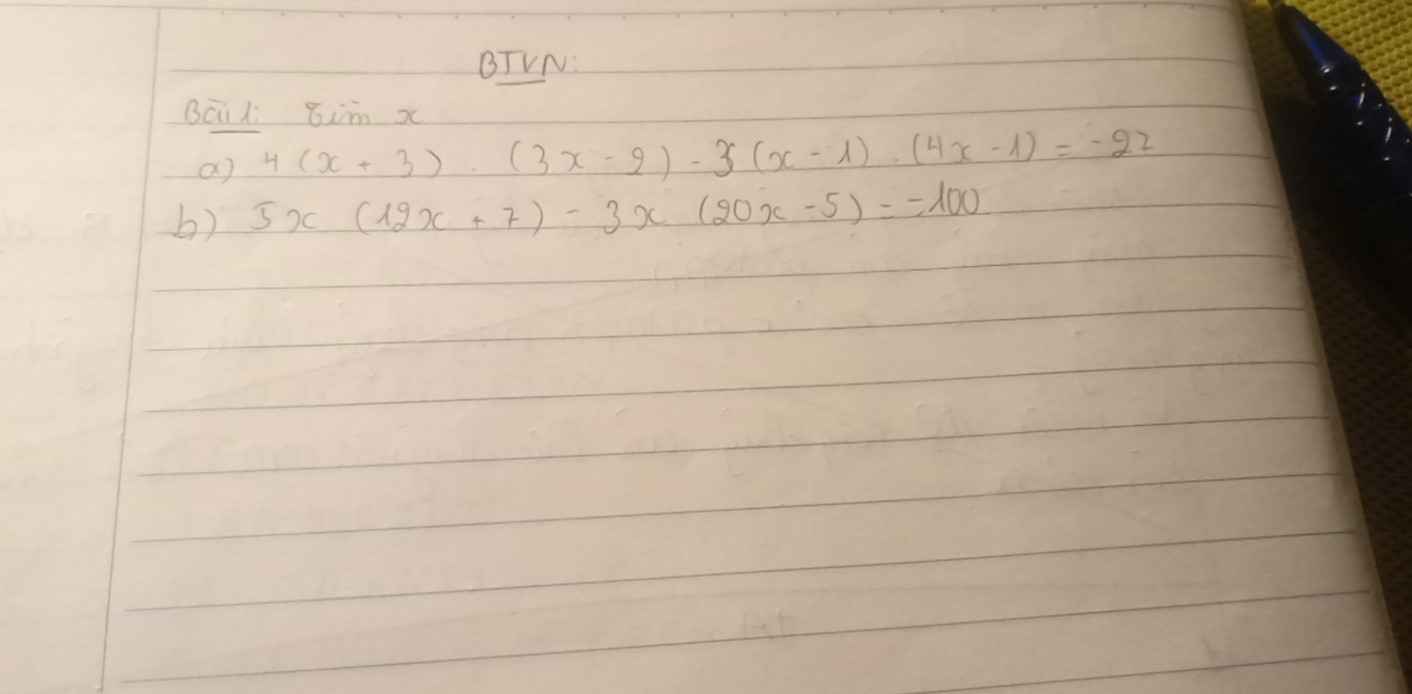



\(a,M=\left(x+1\right)^3-x^3+1-3x\left(x+1\right)\\ =x^3+3x^2+3x+1-x^3+1-3x^2-3x\\ =\left(x^3-x^3\right)+\left(3x^2-3x^2\right)+\left(3x-3x\right)+\left(1+1\right)\\ =2\)
Vậy giá trị của bt không phụ thuộc vào biến
\(b,\left(2x-1\right)^3-6x\left(2x-1\right)^2+12x^2\left(2x-1\right)-8x^3\\ =\left(2x-1\right)^3-3\cdot\left(2x-1\right)^2\cdot2x+3\cdot\left(2x-1\right)\cdot\left(2x\right)^2-\left(2x\right)^3\\ =\left(2x-1-2x\right)^3\\ =\left(-1\right)^3=-1\)
Vậy giá trị của bt không phụ thuộc vào biến
\(c,P=\left(x+y+1\right)^3-\left(x+y-1\right)^3-6\left(x+y\right)^2\\ =\left(x+y+1-x-y+1\right)\left[\left(x+y+1\right)^2+\left(x+y+1\right)\left(x+y-1\right)+\left(x+y-1\right)^2\right]-6\left(x+y\right)^2\\ =2\left[\left(x+y\right)^2+2\left(x+1\right)+1+\left(x+y\right)^2-1+\left(x+y\right)^2-2\left(x+y\right)+1\right]-6\left(x+y\right)^2\\ =2\left[3\left(x+y\right)^2+1\right]-6\left(x+y\right)^2\\ =6\left(x+y\right)^2+2-6\left(x+y\right)^2\\ =2\)
Vậy giá trị của bt không phụ thuộc vào biến