Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

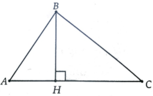
A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)

a, Giả sử tam giác ABC có A ^ < 90 0 kẻ đường cáo BH. Ta có BH=AB.sin A ^
=> S ∆ A B C = 1 2 A C . B H = 1 2 A B . A C . sin A
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có
A
O
B
^
=
α
<
90
0
. Kẻ AH
⊥
BD, tại H và CK
⊥
BD tại K
Ta có: AH = OA.sinα
=> S A B D = 1 2 B D . A H = 1 2 B D . O A . sin α
Tương tự: S C B D = 1 2 B D . C K = 1 2 B D . O C . sin α
=> S A B C D = S A B D + S C B D = 1 2 B D . O A . sin α + 1 2 B D . O C . sin α = 1 2 B D . A C . sin α


Gọi hình bình hành đó là ABCD , từ A kẻ đường cao AH xuống cạnh CD (H thuộc CD)
Ta có : \(AH=AD.sinD\)
\(\Rightarrow S_{ABCD}=CD.AH=CD.AD.sinD\)
Vậy ta có điều phải chứng minh

Gọi Tam giác ABC cho dẽ làm . Kẻ AH vg BC
Tam giác AHB vuông tại H , theo HT giữa cạnh và góc :
AH = AB .sin B
Ta có : \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}AB.sinB.BC\)

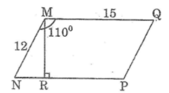
Giả sử hình bình hành MNPQ có MN = 12cm, MQ = 15cm, ∠ NMQ = 1100
Ta có: ∠ NMQ + ∠ MNP = 180 ° (hai góc trong cùng phía)
Suy ra: ∠ MNP = 180 ° - ∠ NMQ
= 180 ° - 110 ° = 70 °
Kẻ MR ⊥ NP
Trong tam giác vuông MNR, ta có:
MR = MN.sin ∠ MNP =12.sin 70 ° ≈ 11,276 (cm)
Vậy S M N P Q = MN.NP ≈ 11,276.15 = 169,14 ( c m 2 )

vì mình không vẽ được hình nên các bạn vẽ hình của bạn nhé
đặt tên : tam giác ABC, AB= a , AC= b , GÓC BAC là \(\alpha\) , kẻ BH vuông góc với AC
tam giác ABH vuông tại H \(\Rightarrow\) \(\sin\alpha\) = \(\frac{BH}{AB}\) \(\Rightarrow\) BH = sin\(\alpha\).AB
có \(s_{ABC}\) = \(\frac{1}{2}BH.AC\)
MÀ BH = sin \(\alpha\) . AB \(\Rightarrow\) S \(_{ABC}\) =\(\frac{1}{2}sin\alpha.AB.AC\) = \(\frac{1}{2}a.b.sin\alpha\) \(\Rightarrow\)đpcm