Ta có (a+2)³-(a+6)(a²+12)+64=a³+6a²+12a+8-a³-12a-6a²-72+64=0(đpcm)

\(\left(a+2^3\right)-\left(a+6\right).\left(a^2+12\right)+64=0\)

\(\Leftrightarrow\left(a+8\right)-\left(a^3+6a^2+12a+72\right)=-64\)

\(\Leftrightarrow\left(a^3+6a^2+12a+72\right)-\left(a+8\right)=64\)

\(\Leftrightarrow a^3+6a^2+11a+64=64\)

\(\Leftrightarrow a^3+6a^2+11a^2=0\)

\(\Leftrightarrow a.\left(a^2+6a+11\right)=0\)

\(\Leftrightarrow a.\left[\left(a^2+2.a.3+9\right)+2\right]=0\)

\(\Leftrightarrow a.\left[\left(a+3\right)^2+2\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=0\\\left(a+3\right)^2+2=0\left(\text{Vô lí}\right)\end{matrix}\right.\)

\(\Rightarrow a=0\)

\(\Rightarrow\) Đpcm.

Có sai đề không bạn

Biểu thức trên có nghiệm mà

\(\Leftrightarrow\left(a+8\right)-\left(a^3+6a^2+12a+72\right)=-64\Leftrightarrow\left(a^3+6a^2+12a+72\right)-\left(a+8\right)=64\)

\(\Leftrightarrow a^3+6a^2+11a+64=64\Leftrightarrow a^3+6a^2+11a=0\Leftrightarrow a\left(a^2+6a+11\right)=0\)

\(\Leftrightarrow a\left[\left(a^2+2.a.3+9\right)+2\right]=0\Leftrightarrow a\left[\left(a+3\right)^2+2\right]=0\Leftrightarrow\orbr{\begin{cases}a=0\\\left(a+3\right)^2+2=0\left(V\text{ô}l\text{í}\right)\end{cases}\Rightarrow a=0}\)

hình như sai đề hay sao ý, có nghiệm mà =)))))

1/ x^3+6x^2+12x+8=0

(x+2)^3=0

x+2=0

x=-2

Vậy x=-2

Điều kiện x ≠ 1 và x  ≠  - 1

Ta có:

Biểu thức dương khi x 2 + 2 x + 3 > 0

Ta có:  x 2 + 2 x + 3  =  x 2 + 2 x + 1 + 2  = x + 1 2 + 2 > 0 với mọi giá trị của x.

Vậy giá trị của biểu thức dương với mọi giá trị x  ≠  1 và x  ≠  - 1

Điều kiện x  ≠  0 và x  ≠  -3

Ta có:

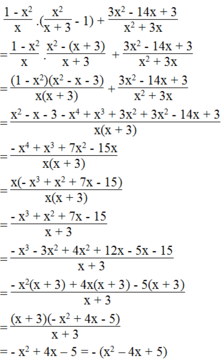
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên

- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.

Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x  ≠  0 và x ≠ -3