
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DL
2

Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
0


25 tháng 1 2015
5x + 47y (1)
= 5x + 30y + 17y = 5(x+6y) + 17y.
17y luôn chia hết cho 17. Vậy để (1) chia hết cho 17 <=> x + 6y chia hết 17

TT
19 tháng 2 2020
Nguyễn Linh Chi Vâng ạ, vậy e thử làm cách này, sẽ giải quyết được cả hai chiều, mong cô xem hộ em ạ :
Đặt \(A=6x+11y\), \(B=x+7y\)
Ta có : \(5A+B=5\left(6x+11y\right)+\left(x+7y\right)=31x+62y\)
Rõ ràng thấy, \(5A+B⋮13\forall x,y\inℤ\). Do đó :
+) Nếu \(A⋮31\)thì \(5A⋮31\) \(\Rightarrow B⋮31\)
+) Nếu \(B⋮31\) thì \(5A⋮31\) mà \(\left(5,31\right)=1\) nên \(A⋮31\)
Vậy : bài toán được chứng minh !!

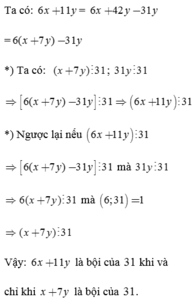
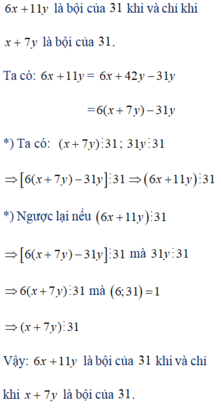
abcabc = abc . 1001 = abc . 13 . 77 chia hết cho 77
=> abcabc chia hết cho 77 (đpcm)
Vì x+15 là bội của x+3
=> x+3+12 chia hết cho x+3
Vì x+3 chia hết cho x+3
=> 12 chia hết cho x+3
=> x+3 thuộc Ư(12)
Mà x là số tự nhiên
=> x > 0
=> x+3 > 3
=> x+3 \(\in\){3; 4; 6; 12}
KL: x \(\in\){0; 1; 3; 9}
Ta có: 77 = 7 x 11
abcabc = abc x 1001
Vì 1001 \(⋮\)7,11 nên abcabc \(⋮\)7,11
Mà (7;11) = 1 và 7 x 11 = 77 nên abcabc \(⋮\)77
\(\Rightarrow\)Đpcm.
Theo bài ra, ta có: x + 15 \(⋮\)x + 3
\(\Leftrightarrow\)(x+3) + 12 \(⋮\)x + 3
Mà x + 3 \(⋮\)x + 3 nên 12 \(⋮\)x + 3.
\(\Rightarrow\)x + 3 \(\in\)Ư(12)
Mà x \(\in\)N nên x \(\in\){1; 2; 3; 4; 6; 12}
Vậy x \(\in\){1; 2; 3; 4; 6; 12}.