B
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 8 2023
Ta có tập xác định của hàm số \(y=cosx\) là \(\mathbb{R}.\)
Nếu với \(x\in\mathbb{R}\) thì \(-x\in\mathbb{R}\) và\(y\left(-x\right)=cos\left(-x\right)=cosx=y\left(x\right).\)
Vậy hàm số \(y=cosx\) là hàm số chẵn.
\(\Rightarrow B\)
PT
1
CM
10 tháng 7 2018
a. Hàm số y = sinx và y = cosx là hàm số tuần hoàn có chu kì là 2 π.
b. Hàm số y = tanx và y = cotx là các hàm số tuần hoàn có chu kì là π.
PT
1
23 tháng 7 2023
a: TXĐ: D=R
Với mọi x thuộc D thì -x cũng thuộc D
\(f\left(-x\right)=-x\cdot cos\left(-x\right)=-x\cdot cosx=-f\left(x\right)\)
=>f(x) lẻ
b: TXĐ: D=R
Với mọi x thuộc D thì -x cũng thuộc D
\(f\left(-x\right)=5\cdot sin^2\left(-x\right)+1=5\cdot sin^2x+1=f\left(x\right)\)
=>f(x) chẵn
c: TXĐ: D=R
Với mọi x thuộc D thì -x cũng thuộc D
\(f\left(-x\right)=sin\left(-x\right)\cdot cos\left(-x\right)=-sinx\cdot cosx=-f\left(x\right)\)
=>f(x) lẻ
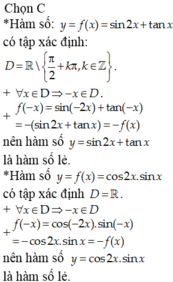
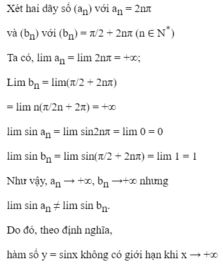
- Hàm số \(y=sin\left(x\right)\)
Tập xác định D = R.
Với mọi \(x\in R\) thì \(-x\in R\) và \(sin\left(-x\right)=-sin\left(x\right)\)
Vậy nên \(y=sin\left(x\right)\) là hàm số lẻ.
- Hàm số \(y=cot\left(x\right)\)
Tập xác định \(D=R\backslash\left\{k\pi,k\in R\right\}\)
Với mọi \(x\in R\) thì \(-x\in R\) và \(cot\left(-x\right)=-cot\left(x\right)\)
Vậy nên \(y=cot\left(x\right)\) là hàm số lẻ.