Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{\Sigma_{cyc}a^3\left(b-c\right)}{\Sigma_{cyc}a^2\left(b-c\right)}=\frac{-\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)}{-\left(a-b\right)\left(b-c\right)\left(c-a\right)}=a+b+c\ge3\sqrt[3]{abc}\)

Đặt \(\left\{{}\begin{matrix}a^2-bc=x\\b^2-ca=y\\c^2-ab=z\end{matrix}\right.\)
\(\Rightarrow x+y+z\ge0\)
\(\)Đẳng thức cần c/m trở thành: \(x^3+y^3+z^3\ge3xyz\left(1\right)\)
Áp dụng Bất đẳng thức AM-GM cho 3 số x,y,z, ta có:
\(x^3+y^3+z^3\ge3\sqrt[3]{x^3.y^3.z^3}=3xyz\)
=> Đẳng thức (1) luôn đúng với mọi x
Dấu = xảy ra khi: x=y=z hay \(a^2-bc=b^2-ca=c^2-ab\)
và \(a^2+b^2+c^2-\left(ab+bc+ca\right)=0\)\(\Rightarrow a=b=c\)

bn tham khảo nha
https://hoc24.vn/cau-hoi/cho-ba-so-thuc-abc-duong-chung-minh-rangsqrtdfraca3a3leftbcright3sqrtdfracb3b3leftcaright3sqrtdfracc3c.5222680437292

Do 5 là số nguyên tố, nên trong 3 nhân tử \(a^3+b^3;b^3+c^3;c^3+a^3\) phải có ít nhất 1 số chia hết cho 5
Không mất tính tổng quát, giả sử \(a^3+b^3⋮5\) \(\Rightarrow a;b\) đều chia hết cho 5 hoặc đều ko chia hết cho 5
Nếu \(a+b\) ko chia hết cho 5:
- a;b đồng dư khi chia 5 \(\Rightarrow\) \(a^3+b^3\) chia 5 dư lần lượt là 2;3;3;2\(\Rightarrow\) ko chia hết cho 5 (ktm)
- a;b khác số dư khi chia 5, do vai trò của a;b là như nhau và a+b ko chia hết cho 5 nên ta có các trường hợp sau:
+ a chia 5 dư 1: nếu b chia 5 dư 2 \(\Rightarrow A\) chia 5 dư -2 (ktm), nếu b chia 5 dư 3 \(\Rightarrow A\) chia 5 dư -3 (ktm)
+ a chia 5 dư 2, b chia 5 dư 4 \(\Rightarrow A\) chia 5 dư 2 (ktm)
+ a chia 5 dư 3, b chia 5 dư 4 \(\Rightarrow A\) chia 5 dư 3 (ktm)
\(\Rightarrow a+b\) ko chia hết cho 5 thì \(a^2+b^2-ab\) cũng ko chia hết cho 5
\(\Rightarrow a^3+b^3\) ko chia hết cho 5 (mâu thuẫn giả thiết)
Vậy \(a+b⋮5\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)⋮5\)
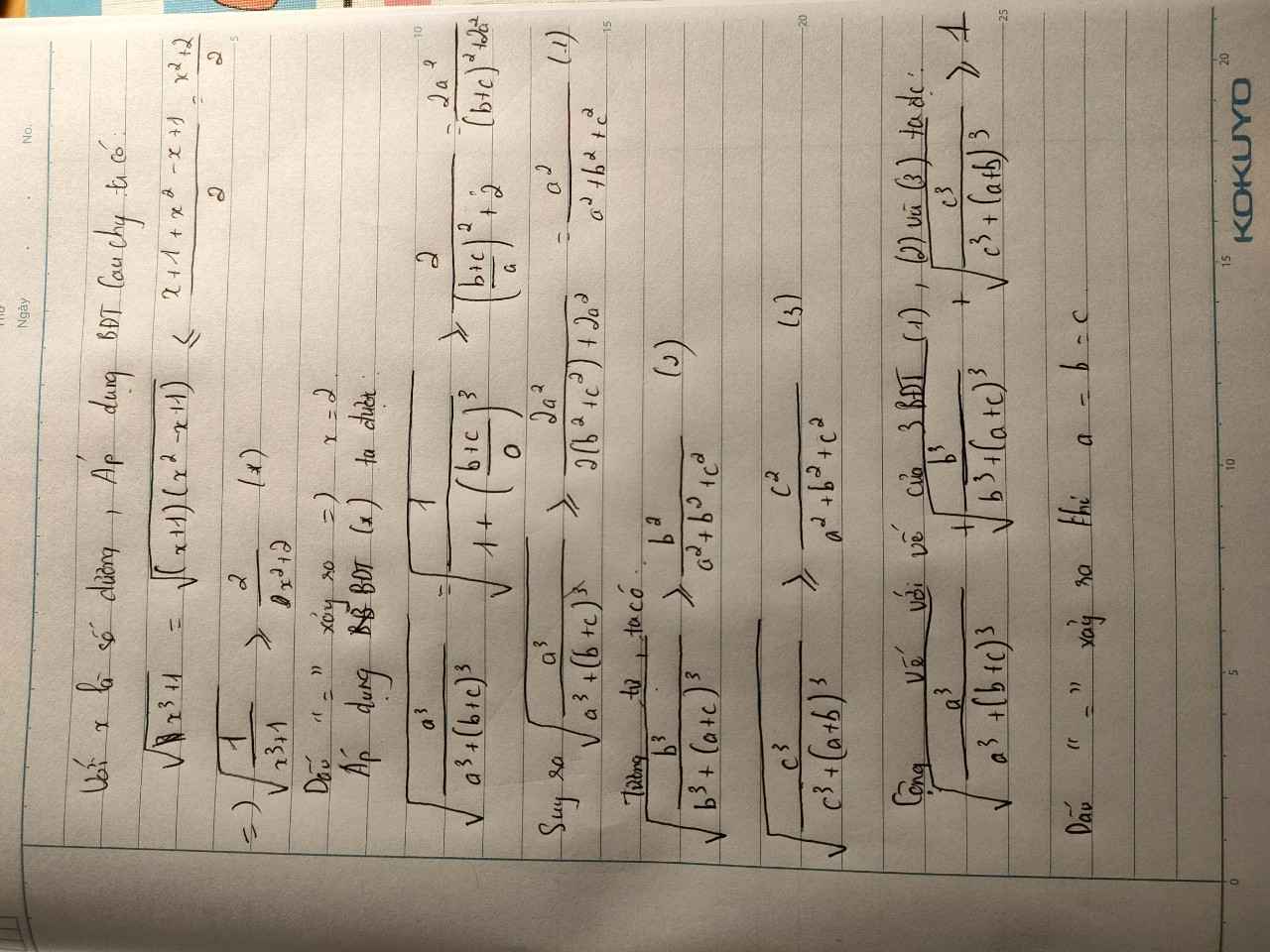
Ta có \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)\)
Áp dụng, ta có \(\left(a+b+c\right)^3-\left(a+b-c\right)^3=\left(a+b+c-a-b+c\right)^3+3\left(a+b+c\right)\left(a+b-c\right)\left(a+b+c-a-b+c\right)=\left(2c\right)^3+3\left(a+b+c\right)\left(a+b-c\right).2c=\left(2c\right)^3+6c\left(a+b+c\right)\left(a+b-c\right)\left(1\right)\)\(\left(b+c-a\right)^3+\left(a+c-b\right)^3=\left(b+c-a+a+c-b\right)^3-3\left(b+c-a\right)\left(a+c-b\right)\left(b+c-a+a+c-b\right)=\left(2c\right)^3-3\left(b+c-a\right)\left(a+c-b\right).2c=\left(2c\right)^3-6c\left(b+c-a\right)\left(a+c-b\right)\left(2\right)\)Từ (1),(2)\(\Rightarrow\left(a+b+c\right)^3-\left(a+b-c\right)^3-\left(b+c-a\right)^3-\left(a+c-b\right)^3=\left(2c\right)^3+6c\left(a+b+c\right)\left(a+b-c\right)-\left[\left(2c\right)^3-6c\left(b+c-a\right)\left(a+c-b\right)\right]=\left(2c\right)^3+6c\left(a+b+c\right)\left(a+b-c\right)-\left(2c\right)^3+6c\left(b+c-a\right)\left(a+c-b\right)=6c\left(a+b+c\right)\left(a+b-c\right)+6c\left(b+c-a\right)\left(a+c-b\right)=6c\left(a^2+2ab+b^2-c^2+ab+bc-b^2+ac+c^2-bc-a^2-ac+ab\right)=6c\left(4ab\right)=24abc\)Vậy \(\left(a+b+c\right)^3-\left(a+b-c\right)^3-\left(b+c-a\right)^3-\left(a+c-b\right)^3=24abc\)(3)
Ta có a,b,c sẽ có một số lẻ và 2 số chẵn nên \(abc⋮4\Rightarrow24abc⋮96\left(4\right)\)
Từ (3),(4)\(\Rightarrow\left(a+b+c\right)^3-\left(a+b-c\right)^3-\left(b+c-a\right)^3-\left(a+c-b\right)^3⋮96\)
tớ nghĩ là theo nguyên lí ''thỏ'' và''chuồng''