7520 = 4510.530

Ta có: 4510.530 = (9.5)10.530 = 910.510.530 = (32)10.540

=320.(52)20 = 320.2520 = (3.25)20 = 7520

Vế phải bằng vế trái nên đẳng thức được chứng minh

Bài 8:

a) \(2^{225}=\left(2^3\right)^{75}=8^{75}\)

\(3^{150}=\left(3^2\right)^{75}=9^{75}\)

Vì \(8^{75}< 9^{75}\Rightarrow2^{225}< 3^{150}\)

b) \(2^{91}=\left(2^{13}\right)^7=8192^7\)

\(5^{35}=\left(5^5\right)^7=3125^7\)

Vì \(8192^7>3125^7\Rightarrow2^{91}>5^{35}\)

c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)

a: Xét ΔCIA và ΔCIM có

CI chung

IA=IM

CA=CM

Do đó: ΔCIA=ΔCIM

bạn thiếu:

Do đó:△CIA=△CIM(c.c.c)

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có 

BM chung

\(\widehat{ABM}=\widehat{DBM}\)

Do đó: ΔABM=ΔDBM

Suy ra; BA=BD

cảm ơn ạ

a: Xét ΔEAI và ΔECD có

EA=EC

góc AEI=góc CED

EI=ED

=>ΔEAI=ΔECD

=>AI=CD

b: ΔEAI=ΔECD

=>góc EAI=góc ECD

=>AI//CD

c: Xét ΔDAI và ΔBDC có

DA=BD

AI=DC

DI=BC

=>ΔDAI=ΔBDC

d: Xét ΔABC có 

D,E lần lượt là trung điểm của AB,AC

nên DE là đường trung bình

=>DE=1/2BC và ED//BC

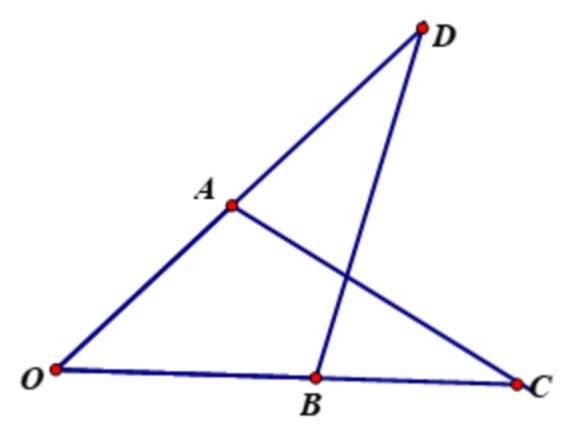
a: Xét ΔOBD và ΔOAC có

\(\widehat{OBD}=\widehat{OAC}\)

OB=OA

\(\widehat{BOD}\) chung

Do đó: ΔOBD=ΔOAC
=>BD=AC; OD=OC

OB+BC=OC

OA+AD=OD

mà OB=OA và OC=OD

nên BC=AD

b: Xét ΔADC và ΔBCD có

AD=BC

CD chung

AC=BD

Do đó: ΔADC=ΔBCD

c: ΔADC=ΔBCD

=>\(\widehat{IDC}=\widehat{ICD}\)

=>ΔIDC cân tại I

=>ID=IC

ID+IB=BD

IC+IA=AC

mà ID=IC và BD=AC

nên IB=IA

d: Xét ΔOAI và ΔOBI có

OA=OB

AI=BI

OI chung

Do đó: ΔOAI=ΔOBI

=>\(\widehat{AOI}=\widehat{BOI}\)

=>OI là phân giác của góc AOB

=>OI là phân giác của góc COD

ΔCOD cân tại O

mà OI là đường phân giác

nên OI\(\perp\)CD

a, xét tam giác OBD và tam giác OAC có:

góc O chung

OA=OB(gt)

góc OAC= góc OBD(gt)

=>tam giác OBD= tam giác OAC (g.c.g)

=>\(\left\{{}\begin{matrix}AC=BD\\OC=OD\end{matrix}\right.\)(2 cạnh tương ứng)

a: Xét ΔOAM và ΔOBM có 

OA=OB

\(\widehat{AOM}=\widehat{BOM}\)

OM chung

Do đó: ΔOAM=ΔOBM

Suy ra: MA=MB

cảm ơn ạ

a: Xét ΔABD và ΔACE có 

\(\widehat{A}\) chung

AB=AC

\(\widehat{ABD}=\widehat{ACE}\)

Do đó: ΔABD=ΔACE

Suy ra: \(\widehat{EBD}=\widehat{ECD}\)

b: Xét ΔADE có AD=AE

nên ΔADE cân tại A

c: Xét ΔABC có

BD là đường phân giác

nên AD/DC=AB/BC=AC/BC(1)

Xét ΔABC có 

CE là đường phân giác

nên AE/EB=AC/BC(2)

Từ (1) và (2) suy ra AE/EB=AD/DC

hay DE//BC

d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)

nên ΔOBC cân tại O

a: Xét ΔBAM và ΔBEM có

BA=BE

\(\widehat{ABM}=\widehat{EBM}\)

BM chung

Do đó: ΔBAM=ΔBEM

b: Ta có: ΔBAM=ΔBEM

nên MA=ME

c: Ta có: ΔBAM=ΔBEM

nên \(\widehat{AMB}=\widehat{EMB}\)

hay MB là tia phân giác của góc AME