Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$P< \frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+....+\frac{1}{199.201}+\frac{1}{201.203}$
$P< \frac{1}{2}(\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+....+\frac{2}{199.201}+\frac{2}{201.203})$
$P< \frac{1}{2}(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{199}-\frac{1}{201}+\frac{1}{201}-\frac{1}{203})$
$P< \frac{1}{2}(\frac{1}{3}-\frac{1}{203})< \frac{1}{2}.\frac{1}{3}=\frac{1}{6}$

Ta có
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\)
...............
\(\dfrac{1}{8^2}< \dfrac{1}{7.8}\)
=> B < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+....+\dfrac{1}{7.8}\)
B < \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
B < \(1-\dfrac{1}{8}< 1\) (Do \(\dfrac{1}{8}>0\))
Vậy.....

\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\)
\(A=\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot...\cdot30\right)^2}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot30}\)
\(A=\dfrac{1\cdot31}{30}=\dfrac{31}{30}\)
Ta có : \(\dfrac{1}{101}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
Do đó :
\(\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{1}{300}+\dfrac{1}{300}..+\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{200}{300}=\dfrac{2}{3}\)
Vậy...

\(B< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{7.8}\)
\(B< 1-\dfrac{1}{8}=\dfrac{7}{8}< 1\)
mink nhanh nhất đó bạn,
ta có :
\(\dfrac{1}{2^2}< \dfrac{1}{1\times2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\times3}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3\times4}\)
. . . . . . .
\(\dfrac{1}{8^2}< \dfrac{1}{7\times8}\)
_________________________________
\(\Rightarrow\)\(B< \)\(\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{7.8}\right)\)
\(\Rightarrow B< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+....+\dfrac{1}{7}-\dfrac{1}{8}\)
\(\Rightarrow B< 1-\dfrac{1}{8}\)
\(\Rightarrow B< 1\)
\(\Rightarrowđpcm\)

a)
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{30^2}\\ < \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{29.30}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{29}-\dfrac{1}{30}\\ =1-\dfrac{1}{30}=\dfrac{29}{30}< 1\left(dpcm\right)\)
b)
\(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{99}+\dfrac{1}{100}=\dfrac{1}{10}+\left(\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)\\ >\dfrac{1}{10}+\dfrac{1}{100}+\dfrac{1}{100}+...+\dfrac{1}{100}=\dfrac{1}{10}+\dfrac{90}{100}\\ =\dfrac{110}{100}>1\left(đpcm\right).\)
c)
\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}\\ =\left(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{9}\right)+\left(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{17}\right)\\ < \dfrac{1}{5}.5+\dfrac{1}{8}.8=1+1=2\left(đpcm\right)\)
d) tương tự câu 1
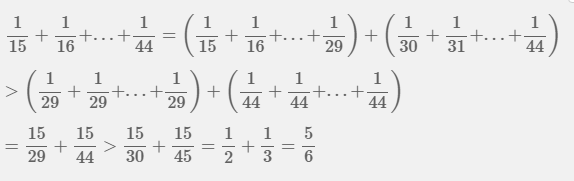
Ta có :\(\dfrac{1}{5}< \dfrac{1}{4};\dfrac{1}{6}< \dfrac{1}{4};\dfrac{1}{7}< \dfrac{1}{4};\dfrac{1}{8}< \dfrac{1}{4}\)
\(\Rightarrow\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{8}< \dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{4}{4}=1\left(1\right)\)
Ta có :\(\dfrac{1}{9}< \dfrac{1}{8};\dfrac{1}{10}< \dfrac{1}{8};\dfrac{1}{11}< \dfrac{1}{8};...;\dfrac{1}{17}< \dfrac{1}{8}\)
\(\Rightarrow\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{17}< \dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+...+\dfrac{1}{8}=\dfrac{8}{8}=1\left(2\right)\)
Từ (1) và (2)\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 1+1=2\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
Ta có : \(\dfrac{1}{5}=\dfrac{1}{5}\), \(\dfrac{1}{6}< \dfrac{1}{5}\), \(\dfrac{1}{7}< \dfrac{1}{5}\),...,\(\dfrac{1}{9}< \dfrac{1}{5}\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{9}< \dfrac{1}{5}\cdot5=1\)
\(\dfrac{1}{10}< \dfrac{1}{8},\dfrac{1}{11}< \dfrac{1}{8},...,\dfrac{1}{17}< \dfrac{1}{8}\)
Vậy \(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{17}< \dfrac{1}{8}\cdot8=1\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{17}< 1+1=2\)
Chúc các bạn học tốt