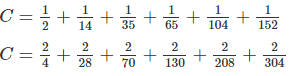Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Tính nhanh:
\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=\dfrac{1}{2}-\dfrac{1}{8}\)
\(=\dfrac{3}{8}\)
2. Tính nhanh
Đặt \(A\) = \(\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{63}+\dfrac{1}{99}+\dfrac{1}{143}\)
\(A\) \(=\dfrac{1}{3.5}+\dfrac{1}{5.7}+\dfrac{1}{7.9}+\dfrac{1}{9.11}+\dfrac{1}{11.13}\)
\(2A=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\)
\(2A=\dfrac{1}{3}-\dfrac{1}{13}\)
\(2A=\dfrac{10}{39}\)
\(A=\dfrac{10}{39}:2\)
\(A=\dfrac{5}{39}\)

1: \(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{11}-\dfrac{1}{13}\right)\)
=1/2*10/39
=5/39
2: \(=\dfrac{5}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{9}-\dfrac{1}{11}\right)=\dfrac{5}{2}\cdot\dfrac{10}{11}=\dfrac{50}{22}=\dfrac{25}{11}\)

Ta có :
\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(C=\dfrac{1}{1.2}+\dfrac{1}{2.7}+\dfrac{1}{7.5}+\dfrac{1}{5.13}+\dfrac{1}{13.16}+\dfrac{1}{16.19}\)
\(C=\dfrac{2}{3}\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+\dfrac{3}{10.13}+\dfrac{3}{13.16}+\dfrac{3}{16.19}\right)\)
\(C=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(C=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)\)
\(C=\dfrac{2}{3}.\dfrac{18}{19}=\dfrac{12}{19}\)
~ Học tốt ~

\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{1\cdot4}+\dfrac{2}{4\cdot7}+\dfrac{2}{7\cdot10}+\dfrac{2}{10\cdot13}+\dfrac{2}{13\cdot16}+\dfrac{2}{16\cdot19}\)
\(=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{16\cdot19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)=\dfrac{2}{3}\cdot\dfrac{18}{19}=\dfrac{12}{19}\)
Ta có :
\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(\Rightarrow C=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4\cdot+4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+\dfrac{3}{13\cdot16}+\dfrac{3}{16\cdot19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\cdot\dfrac{18}{19}\)
\(=\dfrac{12}{19}\)

refer
https://hoc247.net/hoi-dap/toan-6/chung-minh-1-101-1-102-1-103-1-104-1-299-1-300-2-3-faq302038.html

a)
Ta thấy:
\(\dfrac{1}{6}< \dfrac{1}{5}\)
\(\dfrac{1}{7}< \dfrac{1}{5}\)
\(\dfrac{1}{8}< \dfrac{1}{5}\)
\(\dfrac{1}{9}< \dfrac{1}{5}\)
\(\dfrac{1}{11}< \dfrac{1}{10}\)
\(\dfrac{1}{12}< \dfrac{1}{10}\)
\(\dfrac{1}{13}< \dfrac{1}{10}\)
...
\(\dfrac{1}{17}< \dfrac{1}{10}\)
\(\Rightarrow\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 5\cdot\dfrac{1}{5}+8\cdot\dfrac{1}{10}=1+\dfrac{4}{5}=\dfrac{9}{5}< 2\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
b)
Ta thấy:
\(\dfrac{1}{101}>\dfrac{1}{300}\)
\(\dfrac{1}{102}>\dfrac{1}{300}\)
\(\dfrac{1}{103}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{300}>200\cdot\dfrac{1}{300}=\dfrac{2}{3}\)
Vậy \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{300}>\dfrac{2}{3}\)

Câu b hướng làm đó là tách con 1/3 và 1/2 ra thành 50 phân số giống nhau. E tách 1/3=50/150 rồi so sánh 1/101, 1/102,...,1/149 với 1/150. Còn vế sau 1/2=50/100 tách tương tự rồi so sánh thôi
2a.
$\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}$
$< \frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{49.50}$
$=\frac{2-1}{1.2}+\frac{3-2}{2.3}+...+\frac{50-49}{49.50}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{49}-\frac{1}{50}$
$=1-\frac{1}{50}< 1$ (đpcm)

\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{1.4}+\dfrac{2}{4.7}+\dfrac{2}{7.10}+\dfrac{2}{10.13}+\dfrac{2}{13.16}+\dfrac{2}{16.19}\)
\(=\dfrac{2}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{13}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}.\left(1-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}.\dfrac{18}{19}=\dfrac{12}{19}\)