giúp với ;-;

Gọi thời gian vòi 1 ; 2 chảy một mình xong lần lượt là x ; y(ngày) (x;y > 4,8) 

1 giờ vòi 1 chảy  \(\dfrac{1}{x}\)(bể)

1 giờ vòi 2 chảy \(\dfrac{1}{y}\)(bể)

=> 1 giờ 2 vòi chảy \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4,8}\) (1) 

Lại có y - x = 1 (2)

=> Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}y-x=1\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4,8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x+1\\\dfrac{1}{x}+\dfrac{1}{x+1}=\dfrac{1}{4,8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x+1\\x\left(x+1\right)=4,8.\left(2x+1\right)\end{matrix}\right.\)

\(\left\{{}\begin{matrix}5x^2-43x-24=0\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(10x-43\right)^2=2089\\y=x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\sqrt{2089}+43}{10}\\y=\dfrac{\sqrt{2089}+53}{10}\end{matrix}\right.\)

Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.

(Điều kiện: x, y > 80 )

Trong 1 phút vòi thứ nhất chảy được 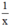 bể; vòi thứ hai chảy được  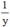bể.

Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:

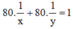
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :

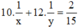
Ta có hệ phương trình:

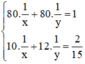
Đặt 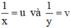 . Khi đó hệ phương trình trở thành :

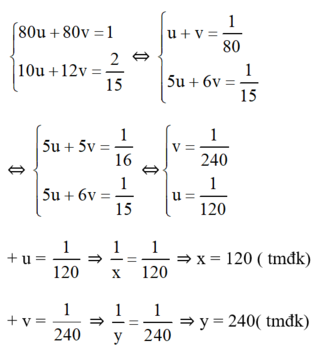
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)

Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.

(Điều kiện: x, y > 80 )

Trong 1 phút vòi thứ nhất chảy được 1/x bể; vòi thứ hai chảy được 1/y bể.

Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:

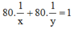
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :

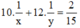
Ta có hệ phương trình:

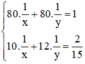
Đặt 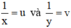 . Khi đó hệ phương trình trở thành :

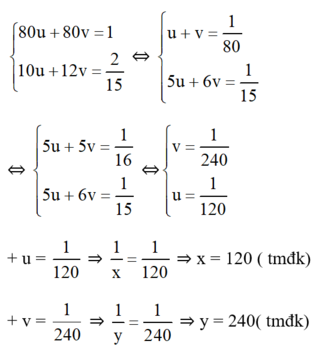
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)

Kiến thức áp dụng

Giải bài toán bằng cách lập hệ phương trình :

Bước 1 : Lập hệ phương trình

- Chọn các ẩn số và đặt điều kiện thích hợp

- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn

- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.

- Từ các phương trình vừa lập rút ra được hệ phương trình.

Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).

Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

thời gian bể 1 chảy là x-1

thời gian bể một chảy trong 1 giờ là \(\frac{1}{x-1}\)

thời gian bể thứ 2 chảy là x

thời gian bể 2 chảy trong 1 giờ là \(\frac{1}{x}\)

4 giờ 48=\(\frac{24}{5}h\)

1 giờ 2 bể chảy \(1:\frac{24}{5}=\frac{5}{24}\left(h\right)\)

ta có pt:

\(\frac{1}{x}+\frac{1}{x-1}=\frac{5}{24}\)

\(24x-24+24x=5x\left(x+1\right)\)

\(48x+24=5x^2-5\)

\(5x^2-48x-29=0\)

\(\sqrt{\Delta}=2\sqrt{721}\)

\(x_1=\frac{48+2\sqrt{721}}{10}=\frac{24+\sqrt{721}}{5}\)

\(x_2=\frac{48-2\sqrt{721}}{10}\left(KTM\right)\)

vòi thứ 1 chảy số giờ là:

\(\frac{24+\sqrt{721}}{5}-1=\frac{19+\sqrt{721}}{5}\left(h\right)\)

Gọi thời gian mà vòi 1 chảy 1 mình đầy bể là x, vòi 2 chảy 1 mình đầy bể là y(x,y>0, đơn vị là h). Theo đề bài ta có:

1 h thì vòi 1 chảy được là \(\dfrac{1}{x}\) (bể); 1 h vòi 2 chảy được là \(\dfrac{1}{y}\) (bể)

Vì 2 vòi cùng chảy vào 1 bể ko có nước thì 6h đầy bể nên ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)

Nếu vòi 1 chảy trong 2h và vòi 2 chảy trong 3 h thì được \(\dfrac{2}{5}h\) nên ta có phương trình: \(\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\left(1\right)\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\left(2\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{3}\left(3\right)\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\left(2\right)\end{matrix}\right.\)

Trừ từng vế của (2) cho (3) ta được:

\(\dfrac{1}{y}=\dfrac{2}{5}-\dfrac{1}{3}\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{15}\Rightarrow y=15\) Thay vào (1) ta được: 

\(\dfrac{1}{x}+\dfrac{1}{15}=\dfrac{1}{6}\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{6}-\dfrac{1}{15}=\dfrac{5-2}{30}=\dfrac{3}{30}=\dfrac{1}{10}\Rightarrow x=10\) 

Vậy ...

Gọi thời gian chảy một mình đầy bể của vòi 1 và vòi 2 lần lượt là a,b

Theo đề, ta có hệ:

1/a+1/b=1/1,5 và 1/4*1/a+1/3*1/b=1/5

=>a=15/4 và b=5/2

  voi thu nhat chay trong 7.5 gio 

voi thu hai chay trong 15 gio