Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn ngẫu nhiên 7 bông hoa tứ 3 bó ta có \(C^7_{21}\) cách.
Chọn 7 bông hoa trong đó số bông hoa hồng bằng số bông hoa ly xảy ra các trường hợp sau :
- Trường hợp 1 : Chọn 7 bông hoa trong đó có 1 bông hoa hồng, 1 bông hoa ly và 5 bông hoa huệ có \(C^1_8C^1_7C^5_6\) cách.
- Trường hợp 2 : Chọn 7 bông hoa trong đó có 2 bông hoa hồng, 2 bông hoa ly và 3 bông hoa huệ có \(C^2_8C^2_7C^3_6\) cách.
- Trường hợp 3 : Chọn 7 bông hoa trong đó có 3 bông hoa hồng, 3 bông hoa ly và 1 bông hoa huệ có \(C^3_8C^3_7C^1_6\) cách.
Từ các trường hợp trên ta có \(C^1_8C^1_7C^5_6+C^2_8C^2_7C^3_6+C^3_8C^3_7C^1_6=12306\) cách chọn 7 bông hoa trong đó số bông hoa hồng bằng số bông hoa ly.
Xác suất cần tính là : \(p=\frac{2015}{19380}\approx0.106\)

Không gian mẫu là số cách chọn ngẫu nhiên 7 hoa từ ba bó hoa gồm 21 hoa.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố “7 hoa được chọn có số hoa hồng bằng số hoa ly”. Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 hoa hồng, 1 hoa ly và 5 hoa huệ nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 2 hoa hồng, 2 hoa ly và 3 hoa huệ nên có ![]() cách.
cách.
● Trường hợp 3. Chọn 3 hoa hồng, 3 hoa ly và 1 hoa huệ nên có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]() .
.
Vậy xác suất cần tính 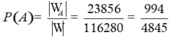
Chọn D.

Đáp án : A
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 7 cách chọn hoa hồng trắng.
Có 5 cách chọn hoa hồng đỏ.
Có 6 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 7.5.6=210 cách.

Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7= 210 cách.
Chọn đáp án B.

Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.
Chọn đáp án B.


Không gian mẫu: \(C_{16}^3\)
a. Số cách chọn 3 bông cùng loại: \(C_5^3+C_7^3+C_4^3=...\)
Xác suất: \(P=\dfrac{C_5^3+C_7^3+C_4^3}{C_{16}^3}=...\)
b. Số cách chọn không có bông nhung nào: \(C_{11}^3\)
Số cách chọn có ít nhất 1 bông nhung: \(C_{16}^3-C_{11}^3\)
Xác suát: \(P=\dfrac{C_{16}^3-C_{11}^3}{C_{16}^3}\)