
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A. Lý thuyết:
Quy tắc cộng hai số nguyên khác dấu:
- Hai số nguyên đối nhau có tổng bằng 0.
- Muốn cộng hai số nguyên khác dấu không đối nhau ta tìm hiệu hai giá trị tuyệt đối của chúng (số lớn trừ số nhỏ) và đặt trước kết quả tìm được dấu của số có giá trị tuyệt đối lớn hơn.
Chú ý: Với mọi số nguyên a ta có: a + 0 = 0 + a = a.
B. Các dạng toán:
Dạng 1: Cộng hai số nguyên
Phương pháp: Áp dụng quy tắc cộng hai số nguyên cùng dấu và quy tắc cộng hai số nguyên khác dấu.
Ví Dụ: Tính a) 26 + (-6) b) (-75) + 50 c) 80 + (-220).
Giải:
a) 26 + (-6) = 20;
b) (-75) + 50 = -25;
80 + (-220) = -140;
Dạng 2: Bài toán đưa về phép cộng hai số nguyên
Phương pháp: Căn cứ vào yêu cầu của đề bài, thực hiện phép cộng hai số nguyên cho trước.
Ví dụ: Tính và nhận xét kết quả:
a) 23 + (-13) và (-23) + 13; b) (-15) + (+15) và 27 + (-27)
Giải:
a) 23 + (-13) =10
(-23) + 13 = -10
Nhận xét: Khi đổi dấu cả hai số hạng thì tổng của chúng cũng tha đổi.
b) (-15) + (+15) = 0
27 + (-27) = 0
Nhận xét: Ta có ngay kết quả bằng 0 vì chúng là các cặp số nguyên đối nhau.
Dạng 3: Điền số thích hợp vào ô trống
Phương pháp: Căn cứ vào quan hệ giữa các số hạng trong một tổng và quy tắc cộng hai số nguyên (cùng dấu, khác dấu), ta có thể tìm được số thích hợp.
Ví dụ: Điều số thích hợp vào ô trống
| a | -2 | 18 | 12 | -5 | |
| b | 3 | -18 | 6 | ||
| a + b | 0 | 4 | -10 |
Bài này các em hãy tự giải, nếu khó khăn hãy nhờ bạn bè, thầy cô, gia sư đang dạy môn toán cho mình để hiểu thêm.
Để củng cố thêm kiến thức gia sư toán lớp 6 sẽ giới thiệu đến các em một số bài tập tự luyện ở dạng cộng hai số nguyên khác dấu:
Bài 1: Tính 5 + 8; (-5) + (-8); 5 + (-8); (-5) + (+8)
Bài 2: Tính:
a) |-15| + (-7)
b) |-42| + |+18|
Bài 3: Dự đoán giá trị của x và kiểm tra lại:
a) x + (-15) = -12;
b) x + (-15) = 12;
c) -7 + x = -18;
d) -7 + x = 18;
Bài 4: Cho a, b là các số nguyên. Chứng minh:
a) Nếu b > 0 thì a + b > a
b) Nếu b <0 thì a + b < a
Bài 5: Chứng minh với mọi số nguyên a, b: |a + b| <= |a| + |b|

Lời giải:
Gọi số cần tìm là $\overline{abc5}$ với $a,b,c$ là STN, $0\leq a,b,c\leq 9; a\neq 0$
Theo bài ra ta có:
$\overline{5abc}=\overline{abc5}-531$
$\Leftrightarrow 5000+\overline{abc}=10\overline{abc}+5-531$
$\Leftrightarrow 9\overline{abc}=5526$
$\overline{abc}=614$
$\Rightarrow \overline{abc5}=6145$
Vậy số cần tìm là $6145$

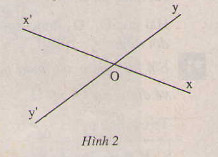
a) Góc xOy và góc ... là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là ... của cạnh Oy'.
b) Góc x'Oy và góc xOy' là ... vì cạnh Ox là tia đối của cạnh ... và cạnh ...
Hướng dẫn giải:
a) Góc xOy và góc x'Oy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'.
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy' là tia đối của cạnh Oy

2n+33n−1∈Z2n+33n−1∈Z
<=> 2n + 3 chia hết cho 3n - 1
<=> 6n + 9 chia hết cho 3n - 1
<=> (6n - 2) + 11 chia hết cho 3n - 1
<=> 2(3n - 1) + 11 chia hết cho 3n - 1
<=> 11 chia hết cho 3n - 1
<=> 3n - 1 thuộc Ư(11) = {±1;±11±1;±11}
Thay từng giá trị vào 3n - 1 để tìm n
Rồi xét giá trị của n có nguyên hay không
Nếu không thì vứt
Nếu là số nguyên thì nhận
\(\dfrac{6n+9}{3n-1}=\dfrac{2\left(3n-1\right)+11}{3n-1}=2+\dfrac{11}{3n-1}\)
\(\Rightarrow3n-1\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
| 3n-1 | 1 | -1 | 11 | -11 |
| n | loại | 0 | 4 | loại |
vậy hả có lớp 1,2,3 không
dep wa