1: Xét ΔABC có AB=AC

nên ΔABC cân tại A

Suy ra: \(\widehat{ABC}=\widehat{ACB}\)

Xét ΔABH và ΔACH có

AB=AC

AH chung

BH=CH
Do đó: ΔABH=ΔACH

Suy ra: \(\widehat{AHB}=\widehat{AHC}\)

mà \(\widehat{AHB}+\widehat{AHC}=180^0\)

nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)

Do đó: AH\(\perp\)BC

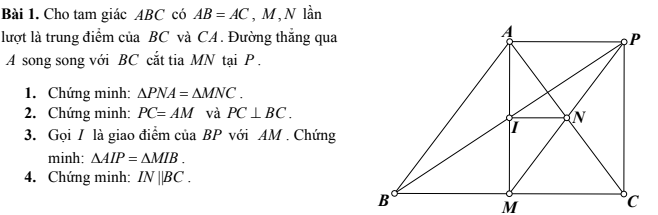
4: Xét ΔAMC có 

I là trung điểm của AM

N là trung điểm của AC

Do đó: IN là đường trung bình của ΔAMC

Suy ra: IN//MC

hay IN//BC

mình chưa học đến đường trung bình

1: Xét ΔABC có AB=AC

nên ΔABC cân tại A

Suy ra: \(\widehat{B}=\widehat{C}\)

Ta có: ΔBAC cân tại A

mà AH là đường trung tuyến ứng với cạnh đáy BC

nên AH là đường cao ứng với cạnh BC

1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)

--> tam giác AOC = tam giác BOD (c.g.c)

--> góc ACO = góc ODB

Mà 2 góc này ở vị trí so le trong

--> AC // BD

b) Tam giác ACD và tam giác BDC có: CD chung; AC = BD (do tam giác AOC = tam giác BOD); góc ACO = góc ODB (câu a)

--> tam giác ACD = tam giác BDC

a) Xét tg ABC có AB=AC(gt)

=> tg ABC cân tại A=> B=C

Cách 1( tính chất  Tg cân)

ta lại có AM là đường trung tuyến

tg ABC là tg cân => AM là dg cao => AH vg góc vs BC

Cách 2 

Xét tg AHB và tg AHC có AH chung

                                        AB=AC( tg ABC cân]
                                        BH=HC( H td BC)

=> tg AHB=tg AHC ( c.c.c)=> AHB=AHC( hai góc bằng nhau) 

Mà BHC= 180 độ=> AHB=AHC=180/2=90 độ

=>AH vg góc với BC

b)Ta có CP vg góc với BC (gt)

          MN vg góc với BC( N là chân dg vuông góc)

=> MN// CP( từ vg góc đến song song)

Xét tg MCP và tg PNM có:

IMN=IPC( MN//CP; slt)

MN=CP( gt)

MP chung

=>tg MCP=Tg PMN (c.g.c)

C) Xét tg MIN và tg PIC có 

IMN=IPC( MN//PC; slt]
MN=CP( gt)

MNI=IPC( MN//PC; slt)

=> tg MIN=tg PIC ( g.c.g)

=>NI=IC( 2 cạnh t/ứ)

thank bạn nhiều

1: Xét ΔAOC và ΔBOD có 

OA=OB

\(\widehat{AOC}=\widehat{BOD}\)

OC=OD

Do đó: ΔAOC=ΔBOD

Suy ra: \(\widehat{ACO}=\widehat{BDO}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//BD