Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC

1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC

1. Tam giác AOC và tam giác BOD có: AO = BO; CO = DO: góc AOC = góc BOD (đối đỉnh)
--> tam giác AOC = tam giác BOD (c.g.c)
--> góc ACO = góc ODB
Mà 2 góc này ở vị trí so le trong
--> AC // BD

Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.

1/
Xét tg ABC có AB=AC => tg ABC cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\) (Trong tg cân hai góc ở đáy = nhau)
BH=CH => AH là đường trung tuyến \(\Rightarrow AH\perp BC\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao và đường trung trực)
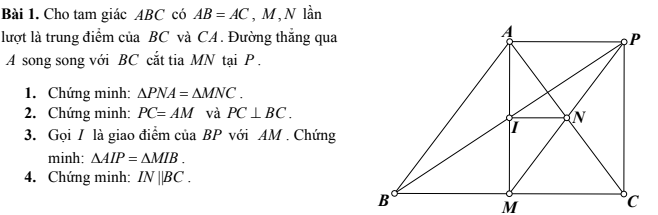
2/ Ta có
\(MN\perp BC;CP\perp BC\) => MN//CP
MN=CP
=> Tứ giác MNPC là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
=> MN=CP; MC=NP; MP chung \(\Rightarrow\Delta MCP=\Delta PMN\left(c.c.c\right)\)
3/
Trong hình bình hành MNPC thì MP và NC là hai đường chéo hbh
=> I là trung điểm của NC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)

bài 2
1)
/2x-7/+\(\dfrac{1}{2}=1\dfrac{1}{2}\)
/2x-7/+\(\dfrac{1}{2}=\dfrac{3}{2}\)
/2x-7/=1
=> 2x-7=1 hoặc -2x+7 =1
2x=8 hoặc -2x=-6
x=4 hoặc x=3
Bài 1:
1: Ta có: \(A=\left(-1\right)^3\cdot\left(-\dfrac{7}{8}\right)^3\cdot\left(-\dfrac{2}{7}\right)^2\cdot\left(-7\right)\cdot\left(-\dfrac{1}{14}\right)\)
\(=\dfrac{7^3}{8^3}\cdot\dfrac{4}{49}\cdot\dfrac{1}{2}\)
\(=\dfrac{343}{512}\cdot\dfrac{2}{49}\)
\(=\dfrac{7}{256}\)

Lời giải:
$4+(y-1)^2\geq 4\Rightarrow \frac{8}{4+(y-1)^2}\leq 2$
Mặt khác, áp dụng BĐT $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-3|=|x-1|+|3-x|\geq |x-1+3-x|=2$
$\Rightarrow |x-1|+|x-2|+|x-3|\geq 2+|x-2|\geq 2$
Vậy $\frac{8}{4+(y-1)^2}\leq 2\leq |x-1|+|x-2|+|x-3|$
Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} (y-1)^2=0\\ (x-1)(3-x)\geq 0\\ x-2=0\end{matrix}\right.\Leftrightarrow y=1; x=2\)
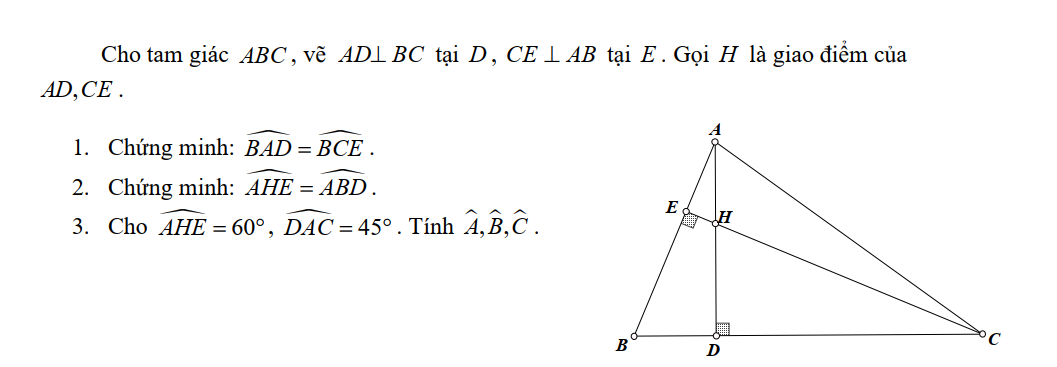


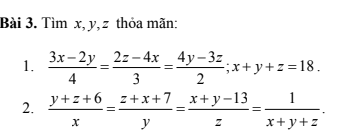




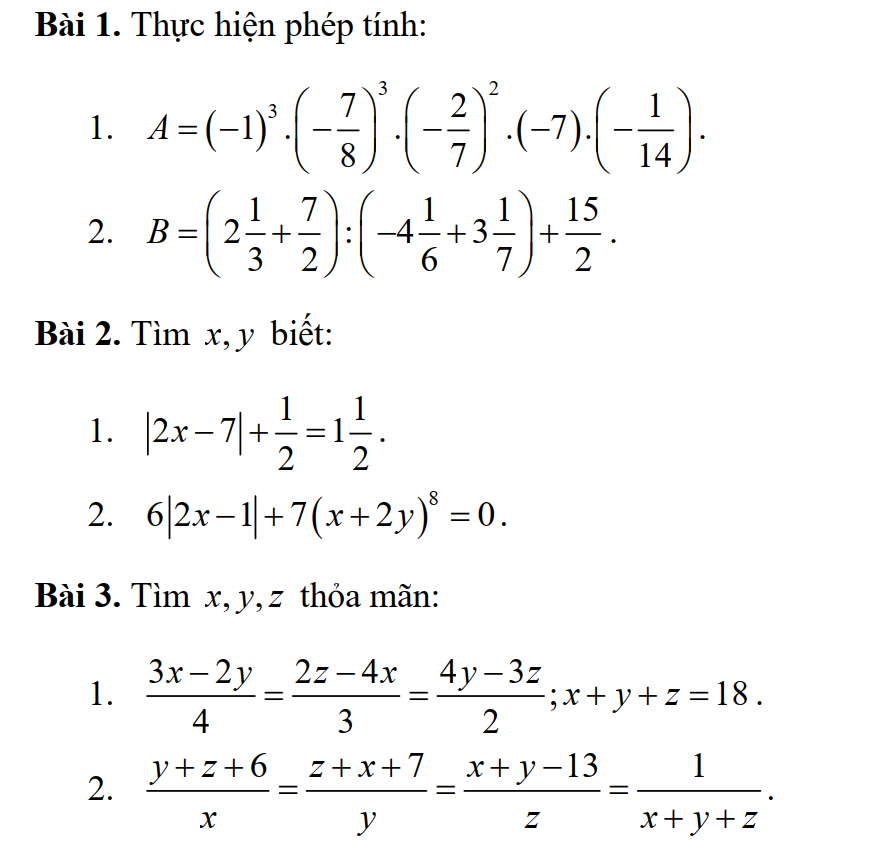
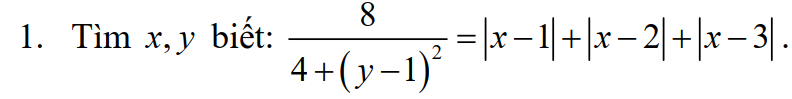
1: Ta có: \(\widehat{BAD}+\widehat{B}=90^0\)
\(\widehat{BCE}+\widehat{B}=90^0\)
Do đó: \(\widehat{BAD}=\widehat{BCE}\)
2: Ta có: \(\widehat{AHE}+\widehat{BAD}=90^0\)
\(\widehat{ABD}+\widehat{BAD}=90^0\)
Do đó: \(\widehat{AHE}=\widehat{ABD}\)
Thế còn câu 3 bạn giúp mình nốt đi