\(\Leftrightarrow\left(5m-2\right)x\le2m^2-m+2\)

- Với \(m=\frac{2}{5}\Rightarrow BPT\) đúng với mọi x \(\Rightarrow\) loại

- Với \(m< \frac{2}{5}\Rightarrow x\ge\frac{2m^2-m+2}{5m-2}\) \(\Rightarrow\) không tồn tại GTLN của x (loại)

- Với \(m>\frac{2}{5}\Rightarrow x\le\frac{2m^2-m+2}{5m-2}\)

Để BPT nhận nghiệm nguyên lớn nhất bằng 1

\(\Rightarrow\frac{2m^2-m+2}{5m-2}< 2\)

\(\Leftrightarrow2m^2-m+2< 10m-4\)

\(\Leftrightarrow2m^2-11m+6< 0\)

\(\Rightarrow\frac{11-\sqrt{73}}{4}< m< \frac{11+\sqrt{73}}{4}\)

\(\Rightarrow m=\left\{1;2;3;4\right\}\)

\(mx^2-2\left(m+2\right)x+2m-1< 0\)

\(< =>mx^2-2\left(m+2\right)x+2m-1\ge0\)

\(a=m\ne0\)

\(\Delta=\left(2m+2\right)^2-4m\left(2m-1\right)\)

\(\Delta=4m^2+8m+4-8m^2+4m\)

\(\Delta=12m-4m^2+4\)

\(< =>\hept{\begin{cases}a>0\\\Delta\le0\end{cases}\hept{\begin{cases}m>0\\12m-4m^2+4\le0\end{cases}\hept{\begin{cases}m>0\\m=\left[\frac{3-\sqrt{13}}{2};\frac{3+\sqrt{13}}{2}\right]\end{cases}}}}\)

\(< =>m=(0;\frac{3+\sqrt{13}}{2}]\)

vậy m vô số nghiệm để bpt vô nghiệm

Ta có:  D = 2 m + 1 1 m 2 − 1 = − 2 m − 1 − m 2 = − m + 1 2

D x = 2 m − 2 1 m 2 − 3 m − 1

= − 2 m + 2 − m 2 + 3 m = − m 2 + m + 2 = m + 1 2 − m

D y = 2 m + 1 2 m − 2 m 2 m 2 − 3 m = 2 m + 1 m 2 − 3 m − m 2 2 m − 2

= − 3 m 2 − 3 m = − 3 m m + 1

Nếu m ≠ − 1 thì hệ phương trình có nghiệm duy nhất

x = D x D = m − 2 m + 1 = 1 − 3 m + 1 y = D y D = 3 m m + 1 = 3 − 3 m + 1

Để x ,   y ∈ Z suy ra 3 m + 1 ∈ Z ,   m + 1 ∈ U , ( 3 ) = ± 1 ; ± 3

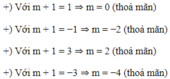
Vậy có 4 giá trị của m thoả mãn đề bài.

Đáp án cần chọn là: D

Đặt t = x + 2 + 2 − x

Điều kiện  t = x + 2 + 2 − x ≥ x + 2 + 2 − x = 2 ⇒ t ≥ 2

Lại có  x + 2 + 2 − x ≤ 1 2 + 1 2 . x + 2 + 2 − x = 2 2 ⇒ t ≤ 2 2

Suy ra 2 ≤ t ≤ 2 2

Ta có: t 2 = 4 + 2 4 − x 2 ⇒ 2 4 − x 2 = t 2 − 4

Phương trình trở thành: t + t 2 − 4 − 2 m + 3 = 0 ⇔ t 2 + t − 2 m − 1 = 0

⇔ t 2 + t − 1 = 2 m *

Xét hàm số f ( x ) = t 2 + t − 1 (parabol có hoành độ đỉnh x = − 1 2 ∉ 2 ; 2 2 ) trên 2 ; 2 2 , có bảng biến thiên

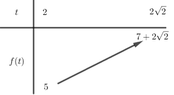
Phương trình (∗) có nghiệm thỏa  2 ≤ t ≤ 2 2  khi  5 ≤ 2 m ≤ 7 + 2 2

⇒ 5 2 ≤ m ≤ 7 + 2 2 2

5 2 ≤ m ≤ 7 + 2 2 2 → 2 , 5 ≤ m ≤ 4 , 91

Vậy có 2 giá trị m nguyên dương là m = 3 ,   m = 4

Đáp án cần chọn là: D

ĐK: \(-2\le x\le2\)

Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\left(2\le t\le2\sqrt{2}\right)\)

Phương trình đã cho trở thành:

\(t+t^2-4+2m+3=0\)

\(\Leftrightarrow2m=f\left(t\right)=-t^2-t+1\)

Phương trình đã cho có nghiệm khi \(minf\left(t\right)\le2m\le maxf\left(t\right)\)

\(\Leftrightarrow-7-2\sqrt{2}\le2m\le-5\)

\(\Leftrightarrow\dfrac{-7-2\sqrt{2}}{2}\le m\le-\dfrac{5}{2}\)

ĐKXĐ: \(x\ge0\)

- Với \(x=0\) không phải nghiệm

- Với \(x>0\) , chia 2 vế của pt cho \(x\) ta được:

\(\dfrac{4x^2+1}{x}+2\sqrt{\dfrac{4x^2+1}{x}}+3-2m=0\)

Đặt \(t=\sqrt{\dfrac{4x^2+1}{x}}\ge\sqrt{\dfrac{2\sqrt{4x^2}}{x}}=2\)

Pt trở thành: \(t^2+2t+3-2m=0\)

\(\Leftrightarrow t^2+2t+3=2m\) (1)

Pt đã cho có nghiệm khi và chỉ khi (1) có nghiệm \(t\ge2\)

Xét hàm \(f\left(t\right)=t^2+2t+3\) khi \(t\ge2\)

Do \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=-1< 2\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge2\)

\(\Rightarrow f\left(t\right)\ge f\left(2\right)=11\)

\(\Rightarrow\) Pt có nghiệm khi \(2m\ge11\Rightarrow m\ge\dfrac{11}{2}\)

Em cảm ơn thầy ạ.