
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

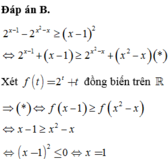

Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.

Lời giải:
Đặt $\sqrt{x^2+1}+x=a$ thì:
$f(a)=e^a-e^{\frac{1}{a}}$
$f'(a)=e^a+\frac{1}{a^2}.e^{\frac{1}{a}}>0$ với mọi $a$
Do đó hàm $f(a)$ là hàm đồng biến hay $f(x)$ là hàm đồng biến trên R
$\Rightarrow f(x)> f(0)=0$ với mọi $x>0$
$\Rightarrow f(\frac{12}{m+1})>0$ với $m$ nguyên dương
Do đó để $f(m-7)+f(\frac{12}{m+1})<0$ thì $f(m-7)<0$
$\Rightarrow m-7<0$
Mặt khác, dễ thấy: $f(x)+f(-x)=0$. Bây h xét:
$m=1$ thì $f(m-7)+f(\frac{12}{m+1})=f(-6)+f(6)=0$ (loại)
$m=2$ thì $f(m-7)+f(\frac{12}{m+1})=f(-5)+f(4)=f(4)-f(5)<0$ (chọn)
$m=3$ thì $f(m-7)+f(\frac{12}{m+1})=f(-4)+f(3)=f(3)-f(4)<0$ (chọn)
$m=4$ thì $f(m-7)+f(\frac{12}{m+1})=f(-3)+f(2,4)=f(2,4)-f(3)<0$ (chọn)
$m=5$ thì $f(m-7)+f(\frac{12}{m+1})=f(-2)+f(2)=0$ (loại)
$m=6$ thì $f(m-7)+f(\frac{12}{m+1})=f(-1)+f(12/7)>f(-1)+f(1)=0$ (loại)
Vậy có 3 số tm

\(1\le1+\sqrt{1-x^2}\le2\Rightarrow3\le3^{1+\sqrt{1-x^2}}\le9\)
Đặt \(3^{1+\sqrt{1-x^2}}=t\Rightarrow t\in\left[3;9\right]\)
Phương trình trở thành: \(t^2-\left(m+2\right)t+2m+1=0\)
\(\Leftrightarrow t^2-2t+1=m\left(t-2\right)\Leftrightarrow m=\dfrac{t^2-2t+1}{t-2}\)
Xét hàm \(f\left(t\right)=\dfrac{t^2-2t+1}{t-2}\) trên \(\left[3;9\right]\)
\(f'\left(t\right)=\dfrac{t^2-4t+3}{\left(t-2\right)^2}\ge0\) ; \(\forall t\in\left[3;9\right]\Rightarrow f\left(t\right)\) đồng biến trên khoảng đã cho
\(\Rightarrow f\left(3\right)\le f\left(t\right)\le f\left(9\right)\Rightarrow4\le m\le\dfrac{64}{7}\)
Có 6 giá trị nguyên của m
Cho e hỏi tại sao điều kiện lại nằm trong khoảng [1,2] vậy ạ ?

ĐKXĐ: \(-x^2+4x+m>0\)
\(log_2\left(-x^2+4x+m\right)-log_2\left(x^2+2\right)< log_23\)
\(\Leftrightarrow log_2\left(\dfrac{-x^2+4x+m}{x^2+2}\right)< log_23\)
\(\Leftrightarrow\dfrac{-x^2+4x+m}{x^2+2}< 3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x^2+4x+m>0\\-x^2+4x+m< 3x^2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>x^2-4x\\m< 4x^2-4x+6\end{matrix}\right.\) ; \(\forall x\in\left[1;5\right]\)
Xét hai hàm \(\left\{{}\begin{matrix}f\left(x\right)=x^2-4x\\g\left(x\right)=4x^2-4x+6\end{matrix}\right.\) trên \(\left[1;5\right]\) ta được: \(\left\{{}\begin{matrix}f\left(x\right)_{max}=f\left(5\right)=5\\g\left(x\right)_{min}=g\left(1\right)=6\end{matrix}\right.\)
\(\Rightarrow5\le m\le6\)
Có 2 giá trị nguyên của m