Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)

Đáp án D
Đặt ![]() theo giả thiết ta có:
theo giả thiết ta có:
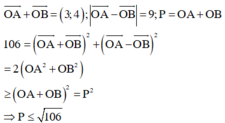
Tổng quát: Với 2 số thực
z
1
,
z
2
thõa mãn ![]()
Khi đó ![]()

Đáp án C
Đặt ![]() Số phức w được biểu diễn bởi điểm M (x;y).
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
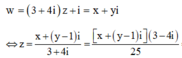
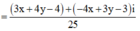
=> |z| = 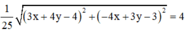
![]()
![]()
![]()
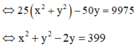
![]()
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: ![]()

Đáp án D
![]()
Ta có:

Dễ thấy tập hợp điểm biểu diễn số phức w là đường tròn tâm (5;7) bán kính 5 13
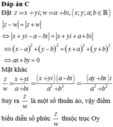


Đáp án B