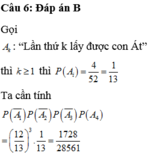
Số số nguyên dương chia hết cho 7 là: \(S_1=\dfrac{994-7}{7}+1=142\)

Số số vừa chia hết cho 7 vừa chia hết cho 5 (nghĩa là chia hết 35): \(S_2=\dfrac{980-35}{35}+1=28\)

Số số vừa chia hết cho 7 vừa chia hết cho 2: \(S_3=\dfrac{994-14}{14}+1=71\)

Số số chia hết cho cả 7;2;5 là: \(S_4=\dfrac{980-70}{70}+1=14\)

Số số thỏa mãn yêu cầu đề bài: \(S_1+S_4-\left(S_2+S_3\right)=57\)

Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇔  0 < a < 333,3

Mà a nguyên nên có 333 số thỏa mãn

Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇔  0 < b < 200

nên có 200 số thỏa mãn 

Số chia hết cho cả 3 và 5 có dạng 15c ta có 0 < 15c ≤ 1000 ⇔  0 < c < 66,6

nên có 66 số thỏa mãn

Do đó số các số thỏa mãn đề bài là 333 + 200 – 66 =467.

Chọn D.

Số chia hết cho 3 có dạng 3a ta có 0  < 3a  ≤ 1000  ⇒ 0< a < 333,3 nên có 333 số thỏa mãn.

Số chia hết cho 5 có dạng 5b ta có 0  < 5b  ≤ 1000  ⇒ 0< b < 200 nên có 200 số thỏa mãn.

Số chia hết cho cả 3 và 5 có dạng 15c ta có  nên có 66 số thỏa mãn.

Do đó số các số thỏa mãn đề bài là 333 + 200 – 66 =467.

Chọn D.

Đáp án B

Chia các chữ số từ 0 đến 9 làm 3 tập: A={0;3;6;9}, B={1;4;7}, C={2;5;8}

\(\Rightarrow\) Có: \(\left(A_4^3-A_3^2\right)+3!+3!+\left(4.3.3.3!-3.3.2!\right)=228\) số có 3 chữ số khác nhau chia hết cho 3

Gọi chữ số có 3 chữ số là \(\overline{abc}\) , ta cần tìm sao cho nó chia hết 15

- TH1: \(c=0\) 

a có 9 cách chọn, với mỗi cách chọn a luôn có 2 cách chọn b sao cho \(a+b⋮3\)

\(\Rightarrow2.9=18\) số

- TH2: \(c=5\) 

+ Nếu a={1;3;4;6;8;9} \(\Rightarrow\)  mỗi cách chọn a có 3 cách chọn b tương ứng \(\Rightarrow6.3=18\) số

+ Nếu a={2;8} \(\Rightarrow\) mỗi cách chọn a có đúng 1 cách chọn b \(\Rightarrow2\) số

Tổng cộng: \(18+18+2=38\) số chia hết cho 15

\(\Rightarrow228-38=190\) số chia hết cho 3 nhưng ko chia hết cho 5

Thầy đừng làm kiểu biến cố đối, thầy làm kiểu trực tiếp đi ạ

a, n(Ω)=20C2=190

b,(A)={ 4; 8; 12; 16; 20}

→n(A)=5

vậy P(A)=5 : 190=1:38

Chọn 2 số thì n(A) sao bằng 5 được ạ

Một số chia hết cho 11 khi thỏa điều kiện: Lấy chữ số đầu tiên trừ cho chữ số thứ 2 rồi cộng cho chữ số thứ 3 rồi trừ cho chữ số thứ 4… Tiếp tục quy luật này đến chữ số cuối cùng, không phân biệt kết quả là số âm hay dương. Nếu kết quả đó chia hết cho 11 thì số ban đầu sẽ chia hết cho 11Một số chia hết cho 11 khi thỏa điều kiện: Lấy chữ số đầu tiên trừ cho chữ số thứ 2 rồi cộng cho chữ số thứ 3 rồi trừ cho chữ số thứ 4… Tiếp tục quy luật này đến chữ số cuối cùng, không phân biệt kết quả là số âm hay dương. Nếu kết quả đó chia hết cho 11 thì số ban đầu sẽ chia hết cho 11

vì vậy ta có số cần tìm là n=11m nếu n có chữ số tận cung là 1 thì ta có

11m \(\equiv\)1(mod10)

\(\Leftrightarrow\)m\(\equiv\)1(mod 10)

vây m=10k+1=>n=110k+11

do n có 6 chữ số nên

10^5\(\le\)110k+11\(\le\)10^6-1

\(\dfrac{10^5-11}{110}\le k\le\dfrac{10^6-12}{110}\)

số số nguyên trong đoạn này là 

\(\left[\dfrac{10^6-12}{110}\right]-\left[\dfrac{10^5-11}{110}\right]+1=9090-908+1=8183\) số chia hết cho 11 tận cùng =1

ta có 111111,.........=> số chữ số tm đề ra nhưng tận cùng =1 là 8183-...

tương tự cho tận cùng =2,=3...=9

3a) Trong 1000 số từ 0 đến 999 có 334 số chia hết cho 3, có dạng 3k, 0 < k < 333.

Suy ra xác suất cần tìm là : \(\frac{334}{1000}\)

b) Trong 1000 số từ 0 đến 999 có 200 số chia hết cho 5, có dạng 5k, 0 < k < 199.

Suy ra xác suất cần tìm là : \(\frac{200}{1000}=\frac{1}{5}\)

sao bn lại ra được 334 số và 200 số ?